Question

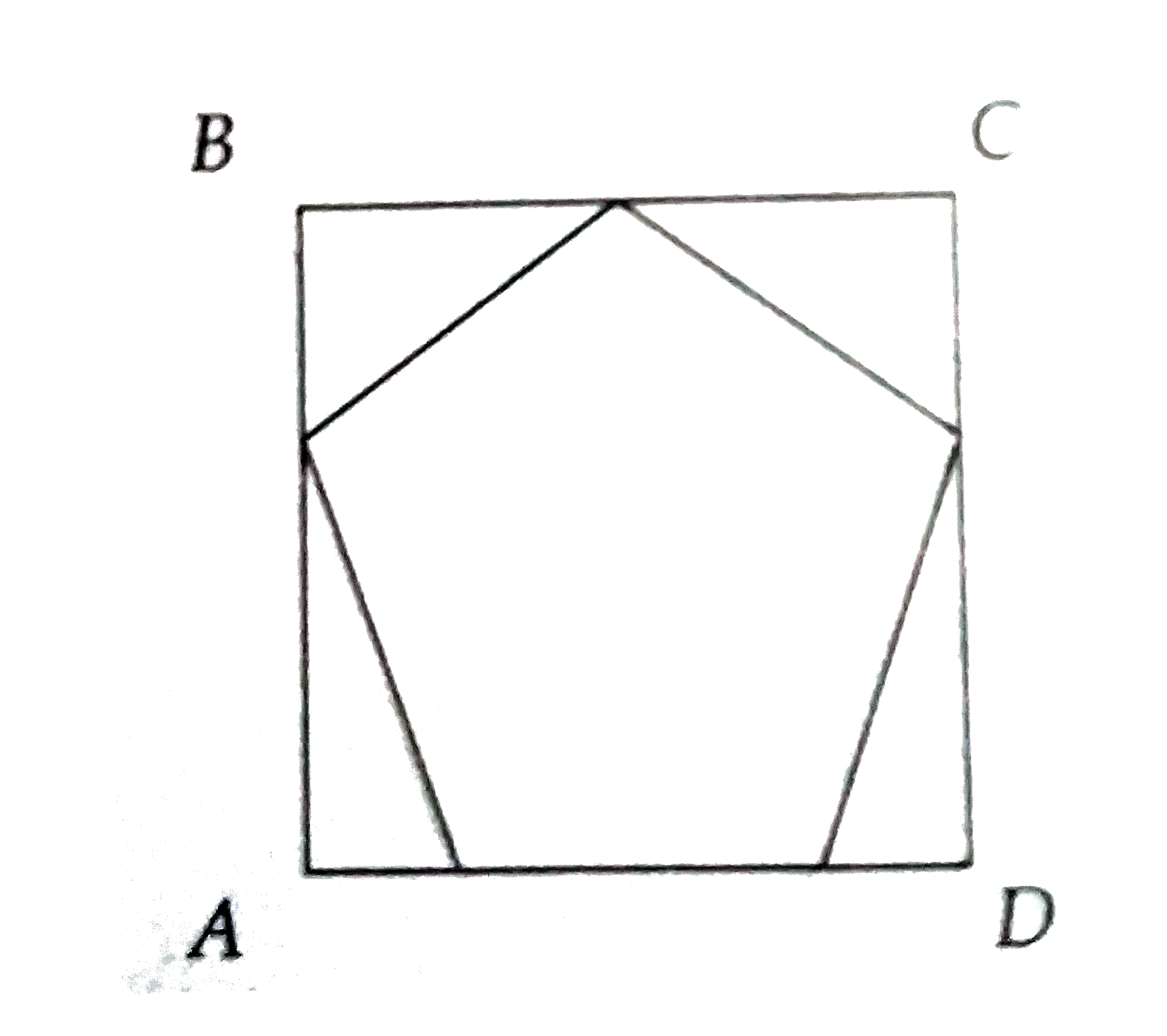
A regular pentagon with all of its vertices on the sides of a rectangle. If $BC=\frac{1}{4}$, what is the perimeter of the pentagon ?

Options

A. `0.31`
B. `0.62`
C. `0.77`
D. `0.80`

Answer

C

Explanation

The angles of the rectangle are right angles. To figure out the interior angles of the pentagon, use the formula for the degree measure of each interior angle of a regular polygon of n sides :
Interior angle `= ((n-2)180)/(n)`
`=((5-2)180)/(5)`
`=180`
Lable all the angles you can :

The angles marked `a^(@)` are equal and together with `108^(@)` add up to `180^(@)`.
`108+2a=180`
`2a=72`
`a = 36`
So the right triangle in the upper left looks like this :

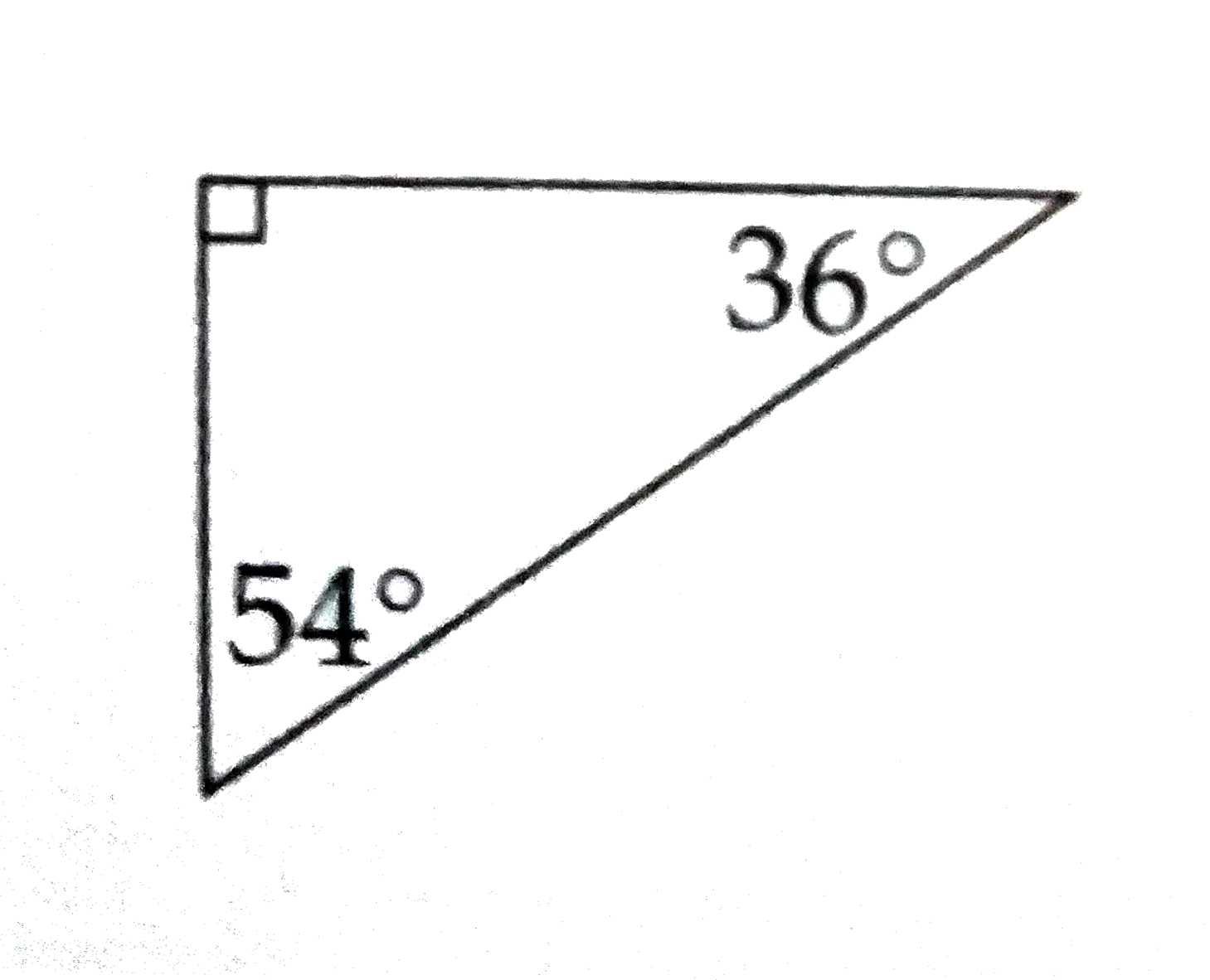
The leg on top (opposite the `54^(@)` angle) is half of BC, or `(1)/(8)`. The hypotenuse of this right triangle is one side of the pentagon whose perimeter you are looking for, so call the hypotenuse x :

You have the leg that's opposite the `54^(@)` and you're looking for the hypotenuse, so use the sine :
`sin 54^(@)=((1)/(8))/(x)`
`x = ((1)/(8))/(sin 54^(@))~~ 0.155`
That's not the answer, however. That's just one side of the pentagon, and you want the perimeter, so multiply that side length by 5 :
Perimeter `~~ 5xx0.155 ~~ 0.77`