If a right circular cylinder of height 10 is inscribed in a sphere of radius 6, what is the volume of the cylinder ?
104
346
545
785
The correct Answer is:B
To find the volume of the right circular cylinder inscribed in a sphere, we can follow these steps:
Step 1: Understand the relationship between the cylinder and the sphere
We have a sphere with a radius of 6 units and a cylinder with a height of 10 units inscribed within it. The cylinder's radius will be determined using the Pythagorean theorem.
Hint: Remember that the height of the cylinder and the radius of the sphere form a right triangle with the radius of the cylinder.
Step 2: Identify the dimensions
The height of the cylinder (h) is given as 10 units. The radius of the sphere (R) is 6 units. The radius of the cylinder (r) is what we need to find.
Hint: The radius of the cylinder can be found using the relationship between the height of the cylinder and the radius of the sphere.
Step 3: Use the Pythagorean theorem
In the right triangle formed by the radius of the sphere, the radius of the cylinder, and half the height of the cylinder, we can express this relationship as:
R2=r2+(h2)2
Substituting the known values:
62=r2+(102)2
36=r2+52
36=r2+25
Hint: Make sure to square the height divided by 2 correctly.
Step 4: Solve for the radius of the cylinder
Rearranging the equation:
r2=36−25
r2=11
Hint: This gives you the square of the radius of the cylinder.
Step 5: Calculate the volume of the cylinder
The volume (V) of a cylinder is given by the formula:
V=πr2h
Substituting the values we have:
V=π(11)(10)
V=110π
Hint: You can approximate π as 3.14 or use the value of π directly if needed.
Step 6: Approximate the volume
Using π≈3.14:
V≈110×3.14
V≈346.4
Thus, the volume of the cylinder is approximately 346 cubic units.
Final Answer: The volume of the cylinder is 110π or approximately 346 cubic units.
We have a sphere with a radius of 6 units and a cylinder with a height of 10 units inscribed within it. The cylinder's radius will be determined using the Pythagorean theorem.
The height of the cylinder (h) is given as 10 units. The radius of the sphere (R) is 6 units. The radius of the cylinder (r) is what we need to find.
In the right triangle formed by the radius of the sphere, the radius of the cylinder, and half the height of the cylinder, we can express this relationship as:
R2=r2+(h2)2
62=r2+(102)2
36=r2+52
36=r2+25
Rearranging the equation:
r2=36−25
r2=11
The volume (V) of a cylinder is given by the formula:
V=πr2h
V=π(11)(10)
V=110π
Using π≈3.14:
V≈110×3.14
V≈346.4
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A right circular cone whose base radius is 4 is inscribed in a sphere of radius 5. what is the ratio of the volume of the cone to the volume of the sphere?
A0.222:1B0.256:1C0.288:1D0.333:1 - Question 2 - Select One
The height and radius of the right circular cylinder below are given in meters. What is the volume, in cubic meters, of the cylinder?
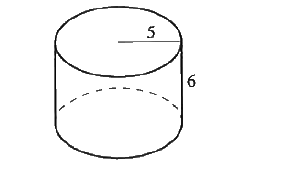 A30πB31πC150πD180π
A30πB31πC150πD180π
The area of the base of a right circular cylinder is 154 cm2 and its height is 15cm. Find the volume of the cylinder.
View SolutionThe area of the base of a right circular cylinder is 154 cm2 and its height is 15cm. Find the volume of the cylinder.
View SolutionA sphere and a right circular cylinder of the same radius have equal volume. By what percentage does the diameter of the cylinder exceed its height ?
View SolutionIf the radius of the base of a right circular cylinder is halved, keeping the height same, what is the ratio of the volume of the reduce cylinder to that of the original.
View SolutionIf the radius of the base of a right circular cylinder is halved, keeping the height same, what is the ratio of the volume of the reduce cylinder to that of the original.
View SolutionIf the radius of the base of a right circular cylinder is halved, keeping the height same, what is the ratio of the volume of the reduce cylinder to that of the original.
View Solution

