What is the area of a triangle whose vertices are (0,6√3),(√35,7), and (0, 3) ?
15.37
17.75
21.87
25.61
The correct Answer is:C
Draw a picture showing the triangle.
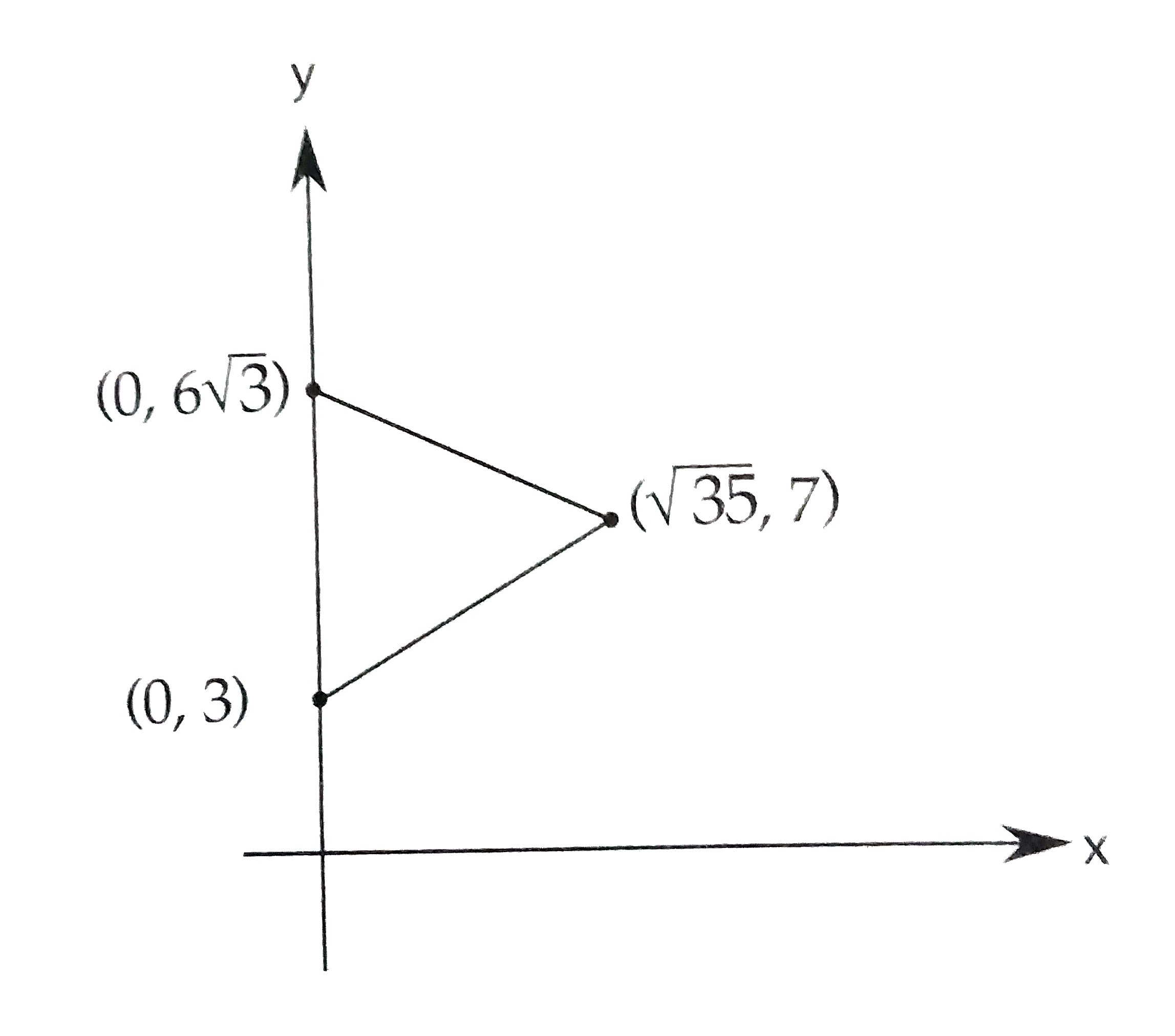
The area of a triangle is 12× base × height. The base of this triangle can be considered to be the side along the y - axis. The length of this side is 6√3−3. The height of this triangle drawn to the side along the y - axis is the distance from the point (√35,7) to the y-axis. This distance is the x - coordinate of the point (√35,7), which is √35. The area of the triangle is 12(6√3−3)(√35)≈21.87.
Topper's Solved these Questions
Similar Questions
Find the area of the triangle whose vertices are: (1,0),(6,0),(4,3)
View SolutionThe orthocentre of a trianlge whose vertices are (0,0),(√3,0)and(0,√6) is
View SolutionOrthocentre of triangle whose vertices are (0,0),(3,4),(4,0) is
View SolutionFind the area of that triangle whose vertices are (2,3),(−3,4)and(7,5).
View SolutionFind the area of triangle, whose vertices are (2,3), (7,5) and (-7,-5).
View SolutionFind the area of the triangle whose vertices are : (3,-4), (7, 5), (-1, 10)
View SolutionFind the area of the triangle whose vertices are: (−3,2),(5,4),(7,−6)
View SolutionDetermine the type (isosceles, right-angled, right-angled isosceles, equilateral, scalence) of the triangles whose vertices are: (1,2√3),(3,0),(−1,0)
View SolutionFind the orthocentre of the triangle whose vertices are (0, 0), (6, 1) and (2, 3).
View SolutionThe incentre of the triangle whose vertices are (-36, 7), (20, 7) and (0, -8) is
View Solution
