A cone has a slant height of 8 and a lateral area of 48π. What is the radius of the base of the cone ?
3
6
12
16
The correct Answer is:B
The lateral area of a cone is determined with the formula A=12cl, where c is the circumference and l is the slant height.
So to find the circumference of the cone, solve the formula for c.
c=2Al
c=2(48π)8=96π8=12π
The circumference of the circular base of a cone is 2πr, where r = radius, so the radius of the base of the cone is 6.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a right circular cone has a lateral surface area of 6π and a slant height of 6, what is the radius of the base ?
A0.50B0.75C1.00D1.25A right circular cone has a volume of 24π cubic inches. If the height of the cone is 2 inches, what is the radius, in inches, of the base of the cone?
A2√3B6C12D36The height of a cone is equal to the radius of its base. The radius of a sphere is equal to the radius of the base of the cone. The ratio of the volume of the cone to the volume of the sphere is
A112B14C13D11

A cylinder is inscribed in a cone with height 30 and base radius 10 , as shown in the above figure . If the radius of the base of the cylinder is 4, what is the height of the cylinder ?
View SolutionA wooden toy is in the shape of a cone mounted on a cylinder as shown alongside.
If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm, find the total surface area of the toy. Take π=3.14]
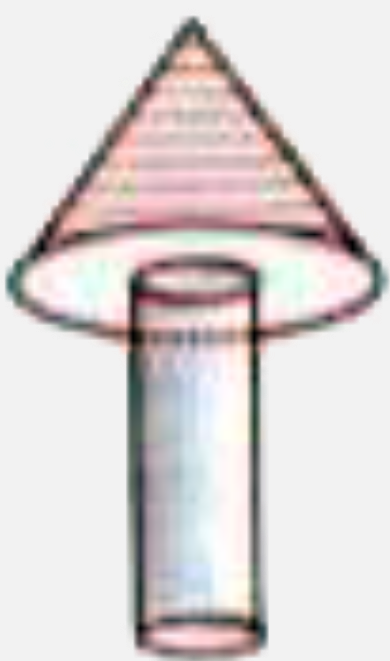
View SolutionA wooden toy is in the shape of a cone mounted on a cylinder as shown alongside If the height of the cone is 24 cm the total height of the toy is 60 cm and the radius of the base of the cone= twice the radius of the base of the cylinder = 10 cm .Find the total surface area of the you.

View SolutionA cylinder with base radius of 8 cm and height of 2 cm is melted to form a cone of height 6 cm. The radius of the cone is
(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 8 cm
View SolutionThe surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
View Solution
