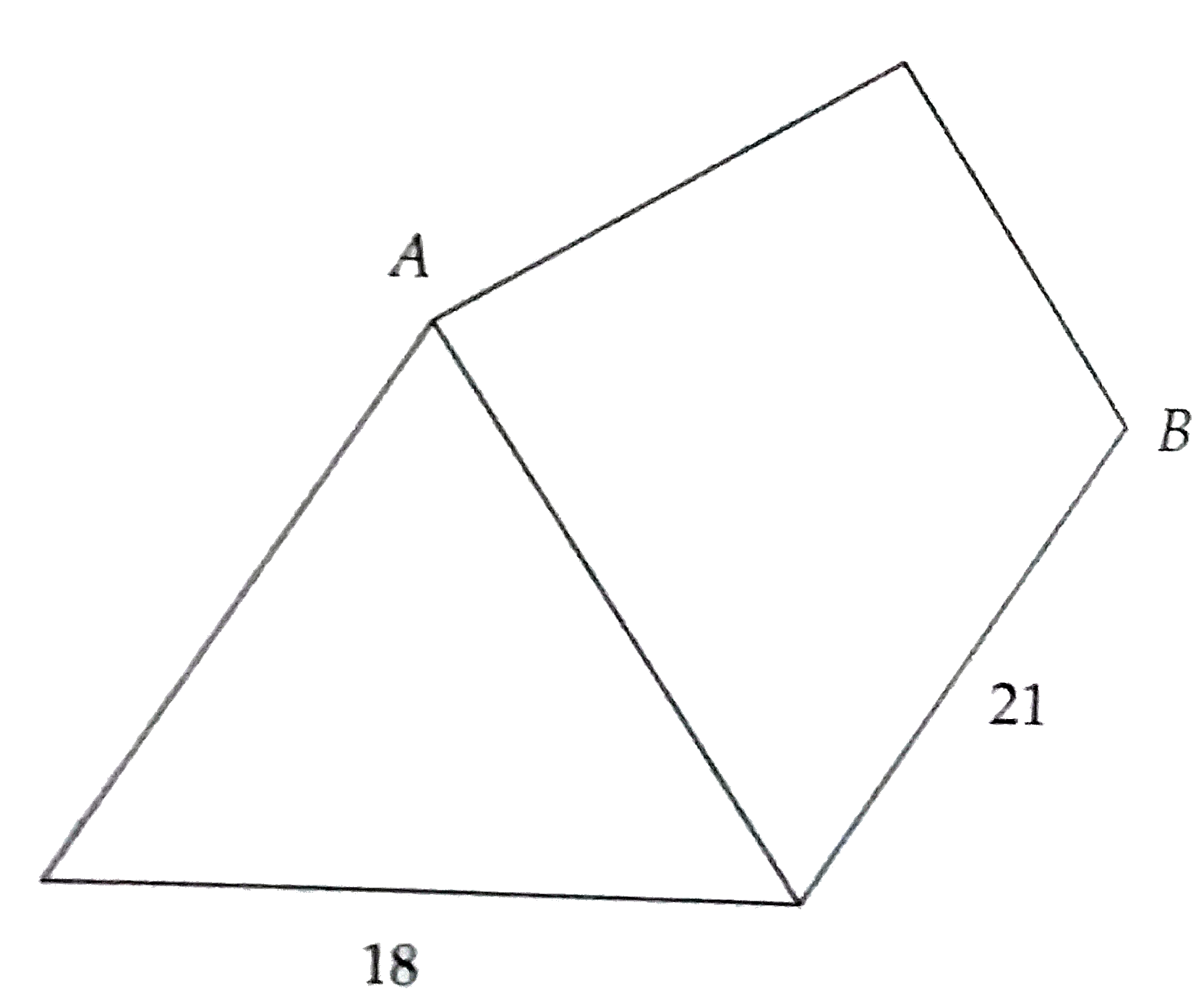
In the triangle solid shown in Figure points A and B are vertices. The triangular faces are isosceles. The solid has a height of 12, a length of 21, and a width of 18. What is the distance between A and B ?
9√5
3√58
3√74
3√85
The correct Answer is:C
You can find the distance by using the distance formula twice. First, calculate the distance from A to the vertex on the bottom right side of the same face. The vertex distance is 12 (the height), and the horizontal distance is 19, since A is above the midpoint of the edge of the solid.
D1=√122+92=√81+144=√225=15
The distance between A and B is the hypotenuse of the right triangle with sides of length 15 and 21. So you can use the distance formula again.
D21=√152+212=√225+441=√666
√666=3√74
Topper's Solved these Questions
Similar Questions
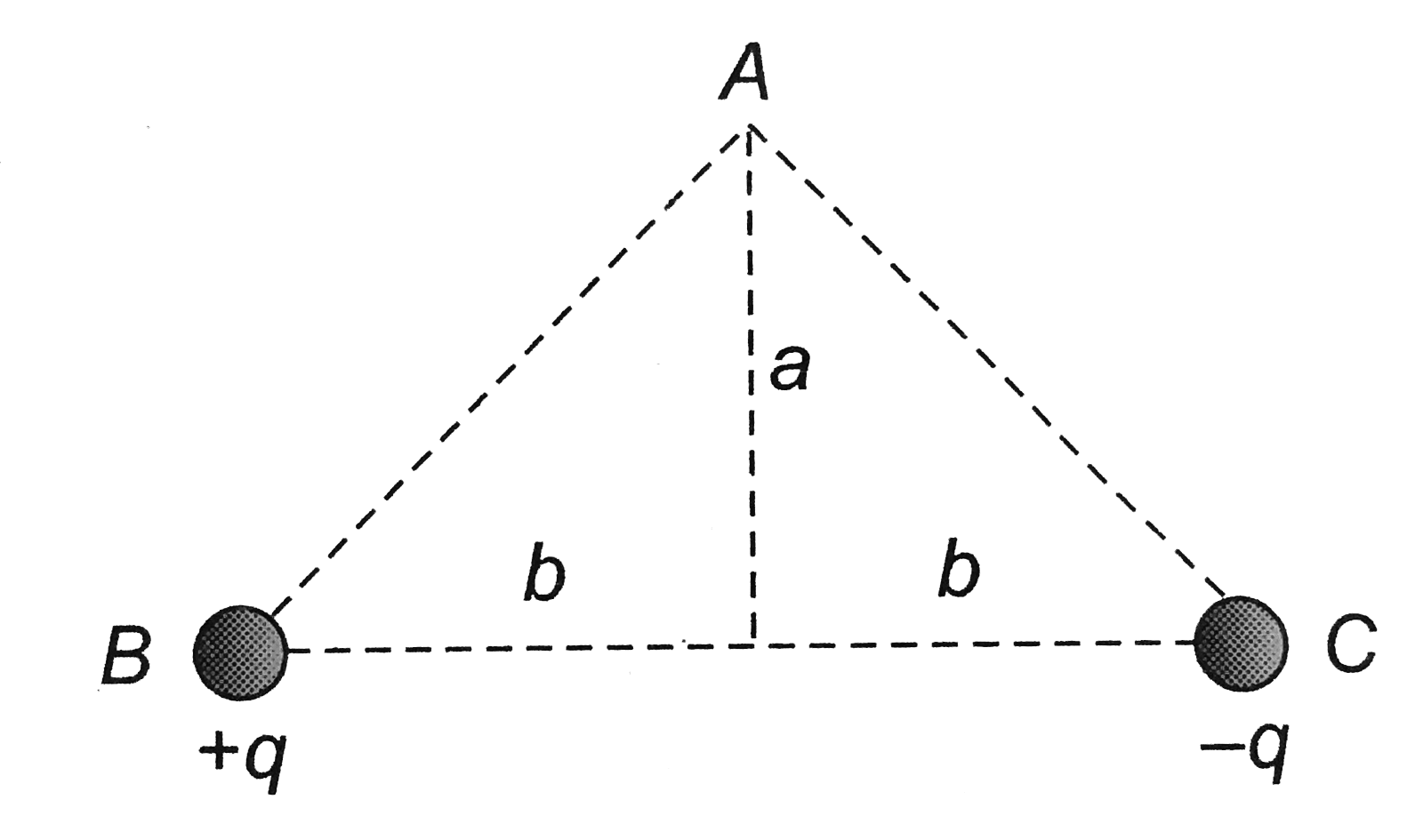
As shown in the figure, charges +qand−q are placed at the vertices B and C of an isoscles triangle. The potential at the vertex A is
View SolutionThree small spheres x,y, and z carry charges of equal magnitudes and with signs shown in fig. They are palced at the vertices of an isosceles triangle with the distance betwwen x and y equal to the distance between x and z. sphere y and z are held in place, but sphere x is free to move on a frictionless surface.
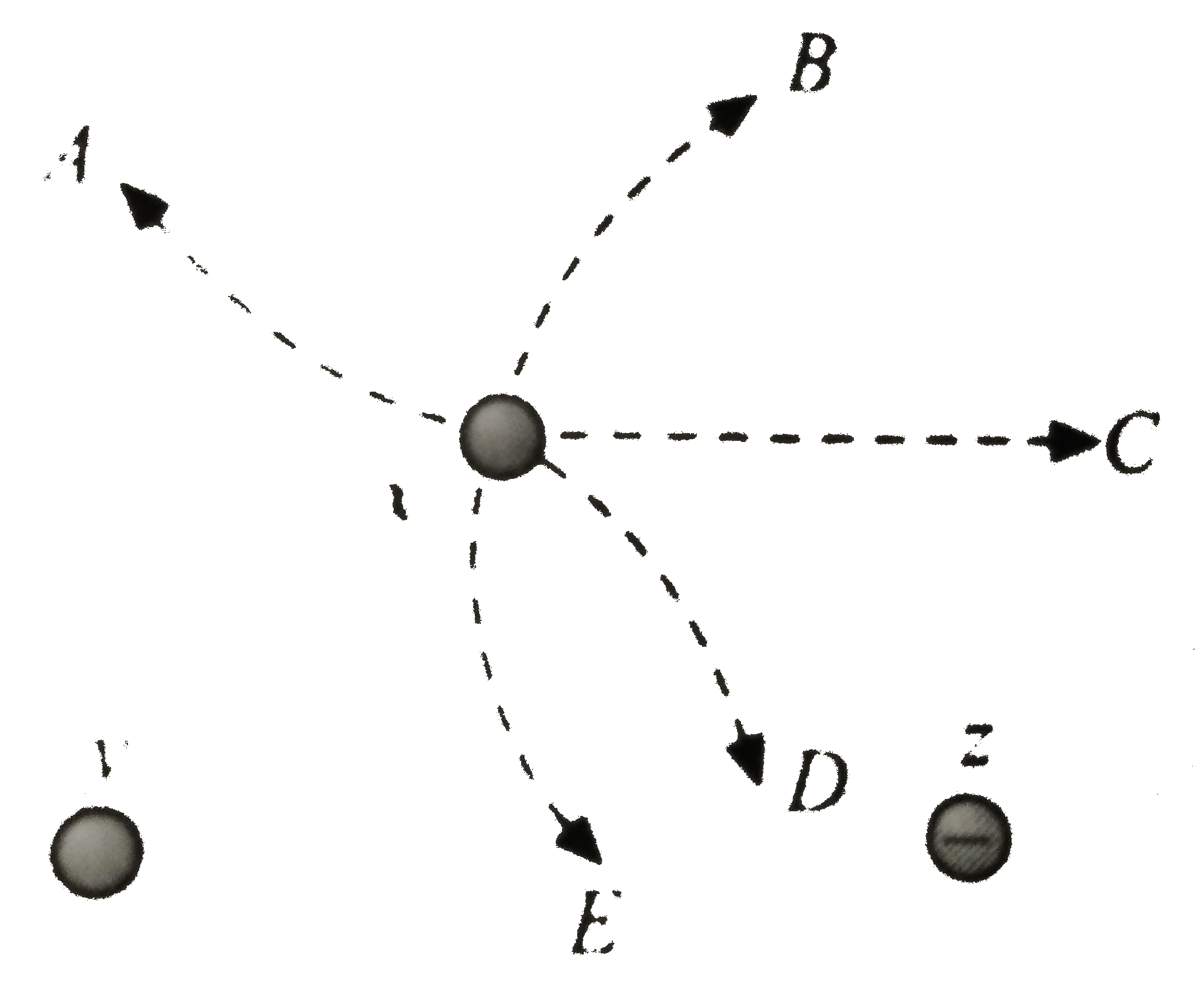
(a) what is the direction of the electric force on sphere x at the point shown in the figure?
(b) Which path is sphere x likely to take when released?
View SolutionIn the circuit shown in figure, each resistance is Net resistance between points A and B is

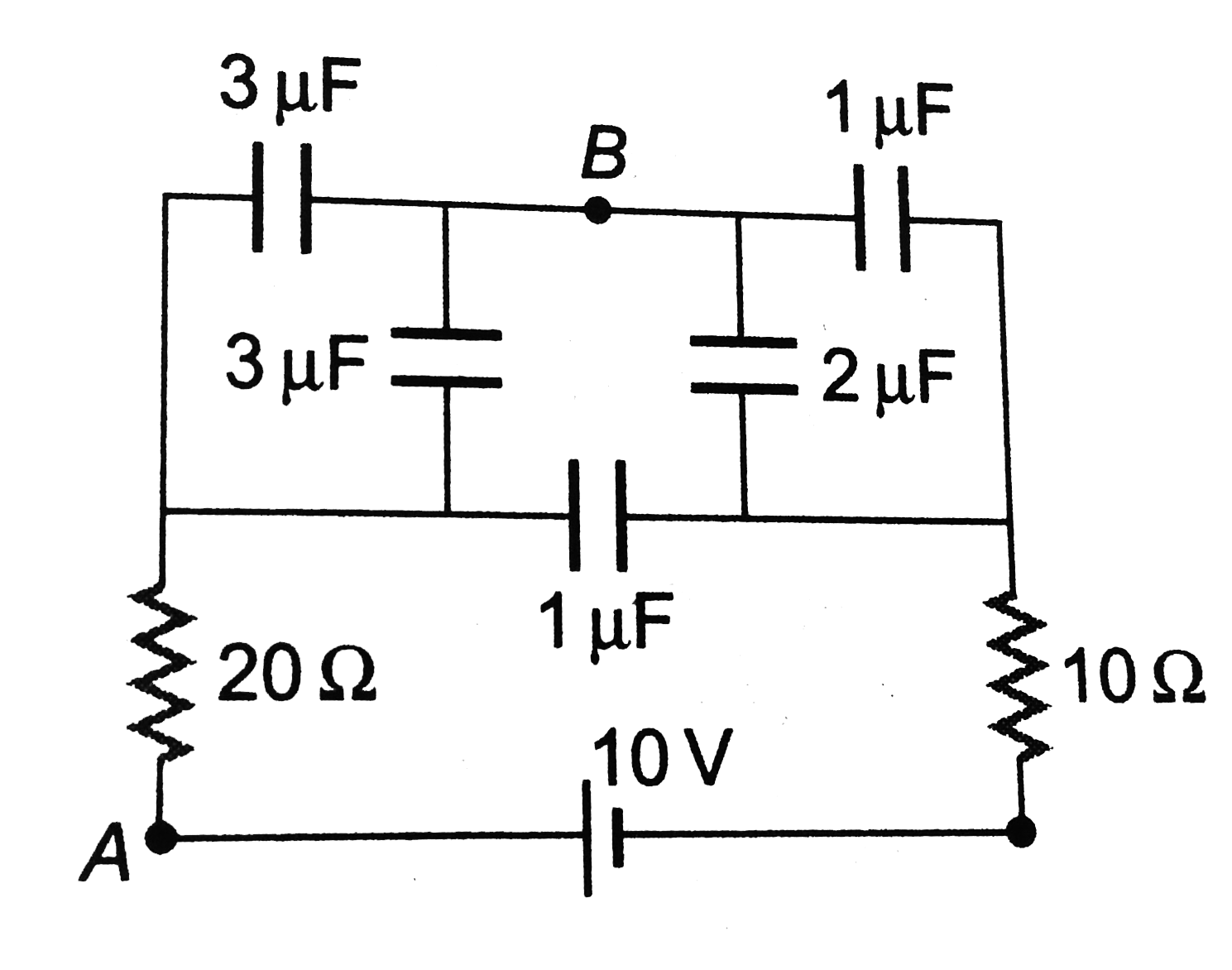
View SolutionIn the circuit shown in figure potential difference between the points A and B in the steady state is
View SolutionThere is a staircase as shown in Figure, connecting points A and B . Measurements of steps are marked in the figure. Find the straight line distance between A and B .
View SolutionProve that the points A(1,−3),B(−3,0)andC(4,1)are the vertices of a right angled Isosceles triangle
View SolutionTwo climbers are at points A and B on a vertical cliff face. To an observer C, 40 m from the foot of the cliff, on the level ground . A is at an elevation of 48∘ and B of 57∘ . What is the distance between the climbers ?
View SolutionShow that the points A(-5,6) ,B(3,0) and C(9,8) are vertices of an isosceles right angled triangles. Find the area of this triangles.
View SolutionFind the equivalent resistance of the circuit shown in figure between the points a and b.Each resistor has a resistances r.

View SolutionFind the equivalent resistance of the circuits shown in figure between the points a and b. Each resistor has a resistance r.


View Solution
