There is a staircase as shown in Figure, connecting points A and B . Measurements of steps are marked in the figure. Find the straight line distance between A and B .
To find the straight line distance between points A and B on the staircase, we can follow these steps:
Step 1: Determine the horizontal distance (AC)
The horizontal distance (AC) is the sum of the lengths of the steps. According to the measurements provided, we have:
- 2 units for each of the 4 steps.
Calculating the total horizontal distance:
AC=2+2+2+2=8 units
Step 2: Determine the vertical distance (BC)
The vertical distance (BC) is the sum of the heights of the steps. According to the measurements provided, we have:
- 1 unit for the first step,
- 1.6 units for the second step,
- 1.6 units for the third step,
- 1.8 units for the fourth step.
Calculating the total vertical distance:
BC=1+1.6+1.6+1.8=6 units
Step 3: Apply the Pythagorean theorem
Now, we can find the straight line distance (AB) using the Pythagorean theorem, which states:
AB2=AC2+BC2
Substituting the values we found:
AB2=82+62
AB2=64+36
AB2=100
Step 4: Calculate AB
Taking the square root of both sides to find AB:
AB=√100=10 units
Final Answer
The straight line distance between points A and B is:
Distance=10 units
---
The horizontal distance (AC) is the sum of the lengths of the steps. According to the measurements provided, we have:
- 2 units for each of the 4 steps.
AC=2+2+2+2=8 units
The vertical distance (BC) is the sum of the heights of the steps. According to the measurements provided, we have:
- 1 unit for the first step,
- 1.6 units for the second step,
- 1.6 units for the third step,
- 1.8 units for the fourth step.
BC=1+1.6+1.6+1.8=6 units
Now, we can find the straight line distance (AB) using the Pythagorean theorem, which states:
AB2=AC2+BC2
AB2=82+62
AB2=64+36
AB2=100
Taking the square root of both sides to find AB:
AB=√100=10 units
The straight line distance between points A and B is:
Distance=10 units
Topper's Solved these Questions
Similar Questions
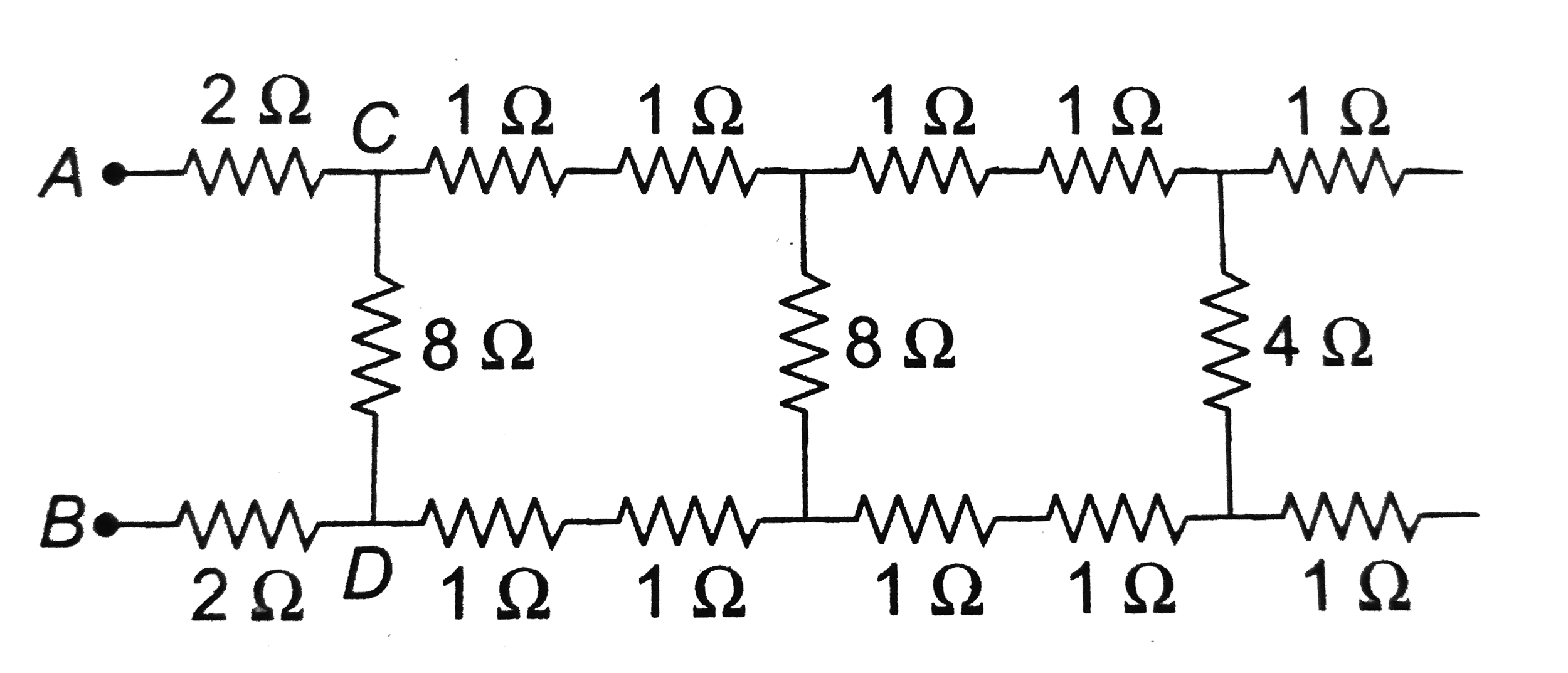
In the figure shown, the total resistance between A and B is
View SolutionIn the figure shown the equivalent capacitance between 'A' and 'B' is :
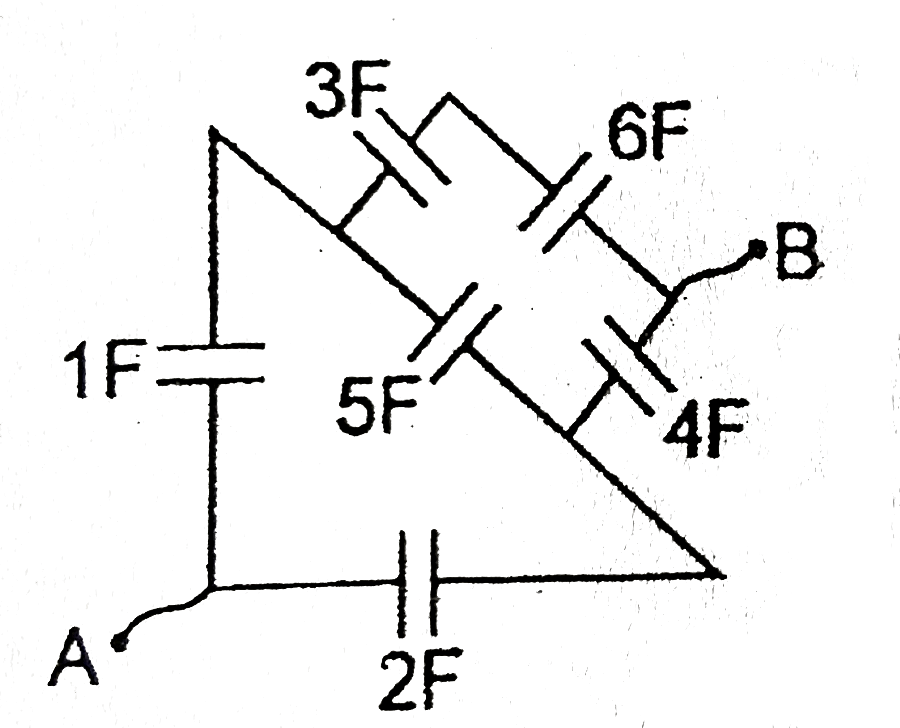
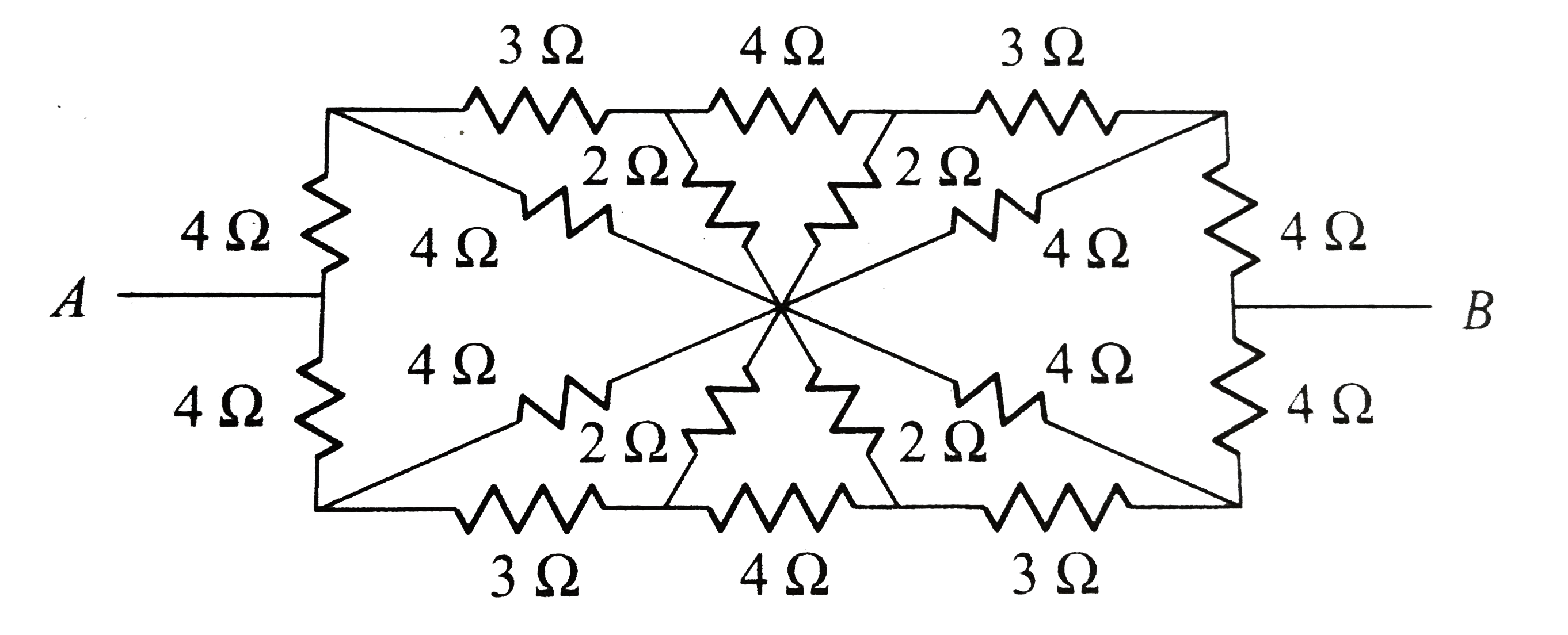
View SolutionA number of resistors are connected as shown in the figure. The equivalent resistance between A and B is
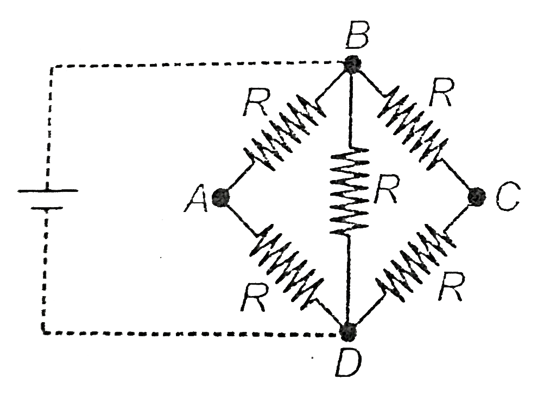
View SolutionRefer to the figure , find equivalent resistance between points B and D.
View SolutionIn the circuit as shown in the figure the effective capacitance between A and B is
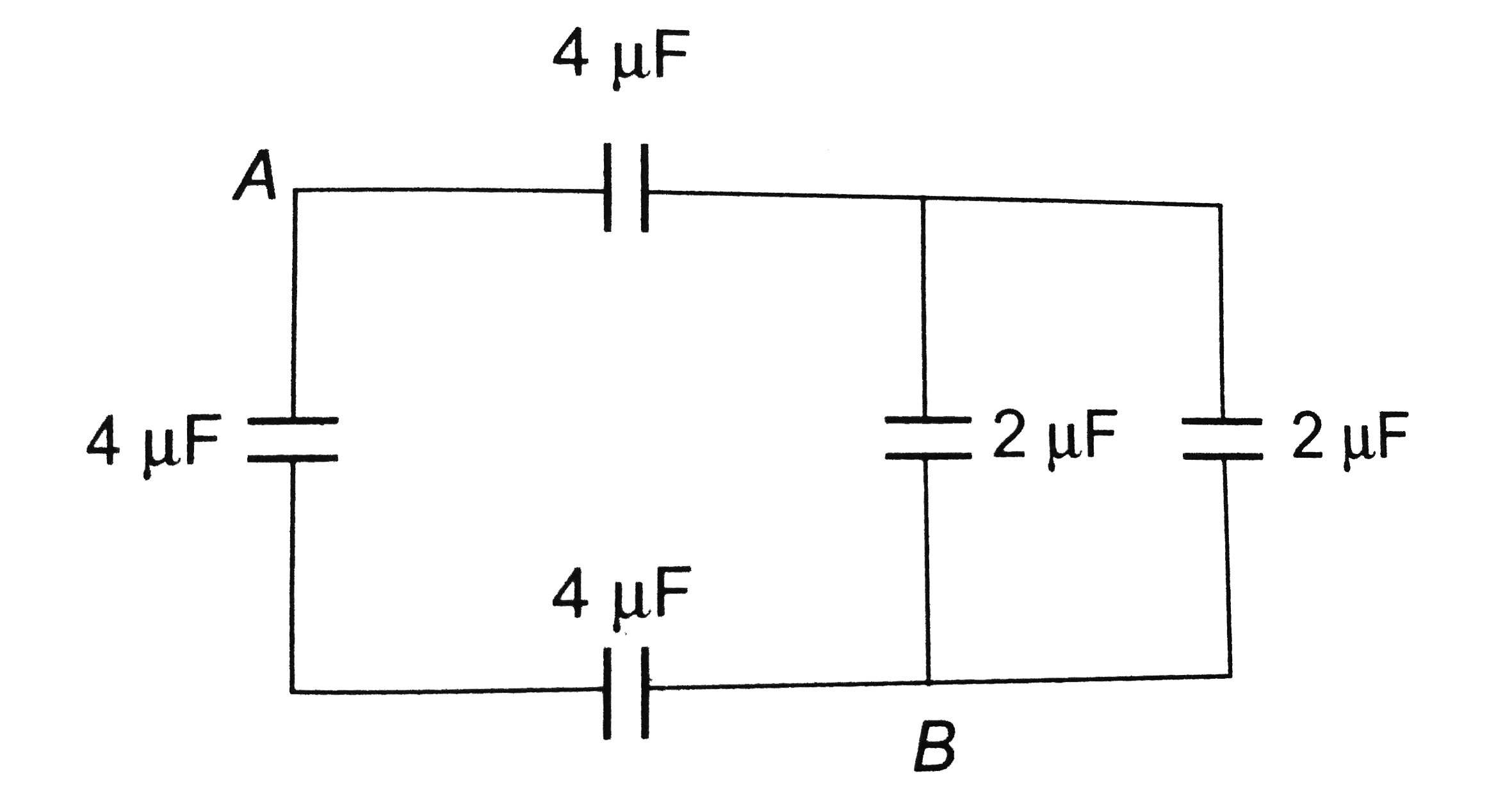
View SolutionIn the circuit as shown in the figure the effective capacitance between A and B is

View SolutionIn the network shown in the figure, the potential difference between A and B is :
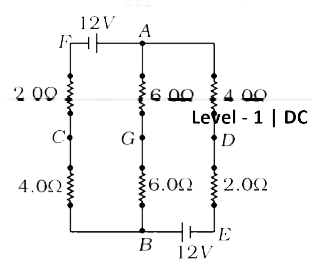
View SolutionThe equivalent capacitance of the circuit as shown in figure between points A and B is
_PHY_E01_019_Q01.png)
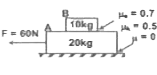
View SolutionIn the figure shown, the force of friction between A and B will be :
View SolutionThe net capacitance of system of capacitance as shown in the figure between points A and B is
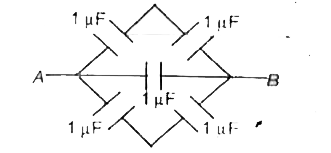
View Solution