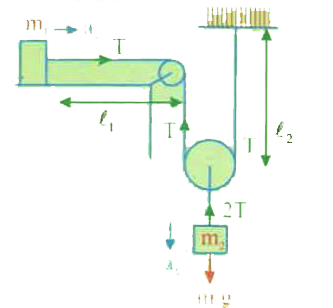
Statement– 1 : In the given fig. a=(m2−m1m1+m2)g
Statement– 2 : In the given fig., T=m1+m22m1m2

Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1.
Statement -1 is False, Statement-2 is True
Statement -1 is True, Statement-2 is False
Step by step video & image solution for Statement– 1 : In the given fig. "a"=(("m"_(2)-"m"_(1))/("m"_(1)+"m"_(2)))"g" Statement– 2 : In the given fig., "T"=("m"_(1)+"m"_(2))/(2"m"_(1)"m"_(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Consider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
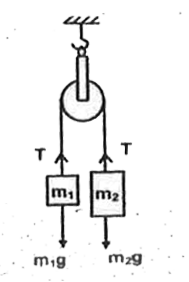
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?A60NB75NC100ND600N - Question 2 - Select One
Consider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
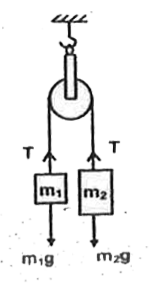
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?A75NB150NC300ND500N - Question 3 - Select One
Consider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
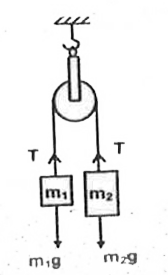
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
If m1=10kg,m2=6kgandg=10m/s2 then what is the acceleration of masses?A2.5m/s2B5m/s2C20m/s2D40m/s2
The value of ∞∑m=1tan−1(2mm4+m2+2) is
View SolutionIn the fig, find the acceleration of m1 and m2
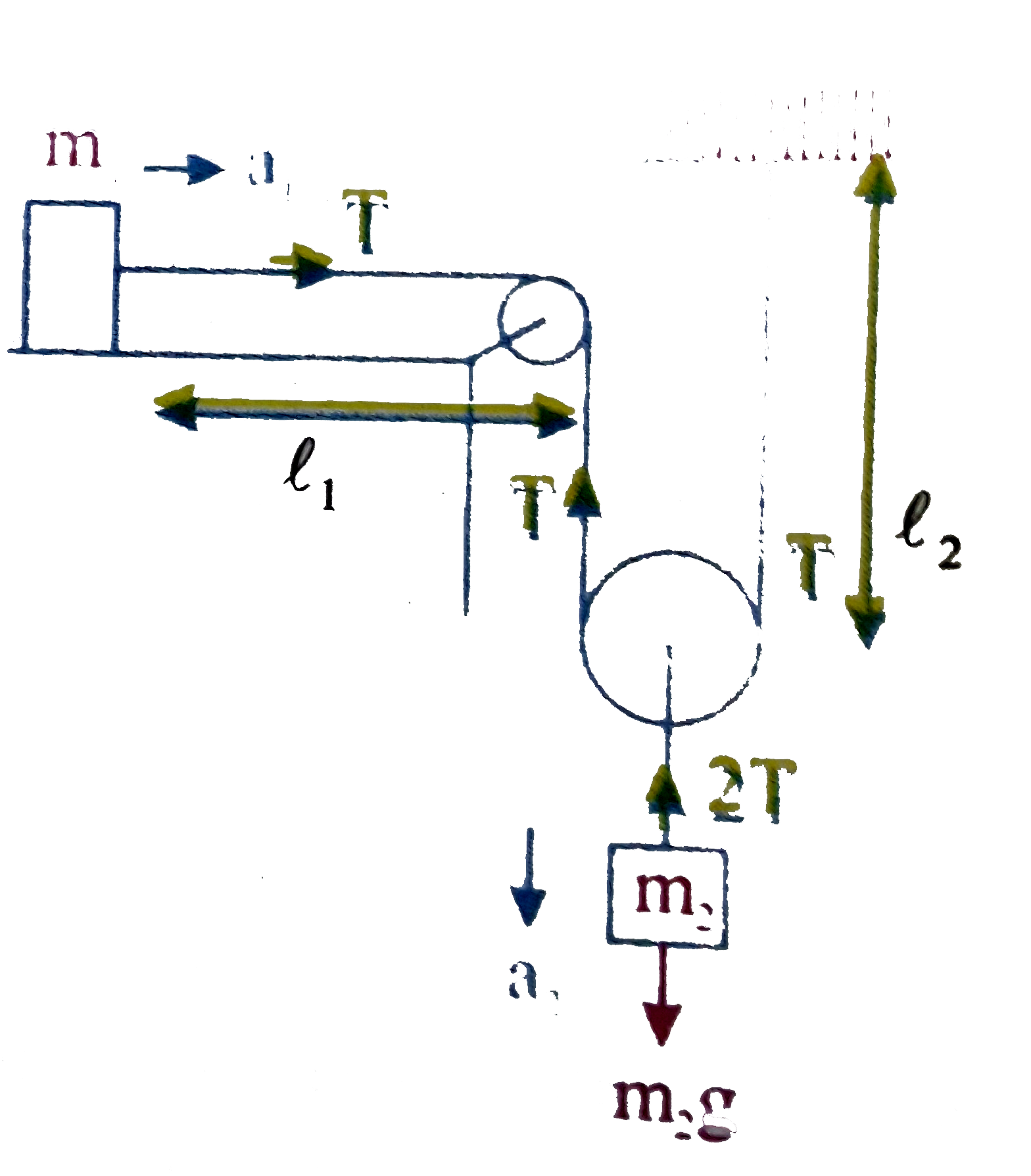 .View Solution
.View SolutionIf m−1m=5 then find m2−1m2
View SolutionShow that in the case of an elastic collision between a particle of mass m1 with a particle of mass m2 initially at rest , (a) the maximum angle through which m1 can be deflected is given by 1−cos2θm=m22m21 when m1>m2 (b) θ1+θ2=π2 when m1=m2
View SolutionThe value of n∑m=1tan−1(2mm4+m2+2) is :
View Solution