If the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
R[1+1√(μ2+1)]
R[1−1√(μ2−1)]
R[1−2√(μ2+1)]
R[1−1√(μ2+1)]
To solve the problem of finding the maximum height to which the insect can crawl in the bowl, we can follow these steps:
Step 1: Understand the Geometry of the Bowl
The bowl is a hemisphere with radius r. The insect can crawl up the side of the bowl, and we need to find the height h it can reach.
Step 2: Define the Variables
Let:
- y be the vertical height from the bottom of the bowl to the insect's position.
- h be the height above the bottom of the bowl, which can be expressed as h=r−y.
Step 3: Analyze Forces Acting on the Insect
When the insect is at height y:
- The weight of the insect mg acts downwards.
- The normal force N acts perpendicular to the surface of the bowl.
- The frictional force f acts parallel to the surface of the bowl.
Step 4: Resolve Forces
At an angle θ (where θ is the angle between the vertical and the line connecting the center of the bowl to the insect):
- The component of the weight acting perpendicular to the surface: mgcosθ
- The component of the weight acting parallel to the surface: mgsinθ
Step 5: Apply Newton's Second Law
The normal force N balances the perpendicular component of the weight:
N=mgcosθ
The frictional force that allows the insect to climb is given by:
f=μN=μmgcosθ
Step 6: Set Up the Equation
For the insect to climb, the frictional force must balance the parallel component of the weight:
μmgcosθ=mgsinθ
Dividing both sides by mg gives:
μcosθ=sinθ
Thus,
tanθ=1μ
Step 7: Relate y and r
From the geometry of the bowl:
Using the right triangle formed by the radius r, the height y, and the distance from the center to the insect:
tanθ=y√r2−y2
Step 8: Substitute tanθ
Now substituting tanθ into the equation:
y√r2−y2=1μ
Step 9: Cross Multiply and Rearrange
Cross multiplying gives:
y=√r2−y2μ
Squaring both sides:
y2=r2−y2μ2
Rearranging gives:
y2+y2μ2=r2μ2
Step 10: Factor Out y2
Factoring out y2:
y2(1+1μ2)=r2μ2
Step 11: Solve for y
Thus,
y2=r2μ2(1+1μ2)
y=r√1+μ2
Step 12: Calculate Maximum Height h
Now substituting back to find h:
h=r−y=r−r√1+μ2
h=r(1−1√1+μ2)
Final Answer
The maximum height h to which the insect can crawl in the bowl is:
h=r(1−1√1+μ2)
The bowl is a hemisphere with radius r. The insect can crawl up the side of the bowl, and we need to find the height h it can reach.
Let:
- y be the vertical height from the bottom of the bowl to the insect's position.
- h be the height above the bottom of the bowl, which can be expressed as h=r−y.
When the insect is at height y:
- The weight of the insect mg acts downwards.
- The normal force N acts perpendicular to the surface of the bowl.
- The frictional force f acts parallel to the surface of the bowl.
At an angle θ (where θ is the angle between the vertical and the line connecting the center of the bowl to the insect):
- The component of the weight acting perpendicular to the surface: mgcosθ
- The component of the weight acting parallel to the surface: mgsinθ
The normal force N balances the perpendicular component of the weight:
N=mgcosθ
f=μN=μmgcosθ
For the insect to climb, the frictional force must balance the parallel component of the weight:
μmgcosθ=mgsinθ
μcosθ=sinθ
Thus,
tanθ=1μ
From the geometry of the bowl:
Using the right triangle formed by the radius r, the height y, and the distance from the center to the insect:
tanθ=y√r2−y2
Now substituting tanθ into the equation:
y√r2−y2=1μ
Cross multiplying gives:
y=√r2−y2μ
y2=r2−y2μ2
y2+y2μ2=r2μ2
Factoring out y2:
y2(1+1μ2)=r2μ2
Thus,
y2=r2μ2(1+1μ2)
y=r√1+μ2
Now substituting back to find h:
h=r−y=r−r√1+μ2
h=r(1−1√1+μ2)
The maximum height h to which the insect can crawl in the bowl is:
h=r(1−1√1+μ2)
Topper's Solved these Questions
Similar Questions
If the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View SolutionA car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tire and the road is μs=2.0, find the maximum speed the car can take without skidding.
View Solution
Knowledge Check
The coefficient of friction between an insect and a hemispherical bowl of radius r is μ. The maximum height to which the insect can crawl in the bowl is
Ar√1+μ2Br[1−1√1+μ2]Cr√1+μ2Dr[√1+μ2−1]The coefficient of friction between a hemispherical bowl and an insect is √0.44 and the radius of the bowl is 0.6m. The maximum height to which an insect can crawl in the bowl will be
A0.4mB0.2mC0.3mD0.1mThe coefficient of friction between a hemispherical bowl and an insect is √0.44 and the radius of the bowl is 0.6m. The maximum height to which an insect can crawl in the bowl will be .
A0.4mB0.2mC0.3mD0.1m
a hemispherical bowl is made of steel 0.5 cm thick. The inside radius of the bowl is 4 cm. Find the volume of steel used in making the bowl.
View SolutionA partical is placed at rest inside a hollow hemisphare of redius R. The coefficient of friction between the partical and the homisphere is μ=1√3. The maximum height up to which the partical can remain stationary is
View SolutionA particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is
View SolutionAn insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
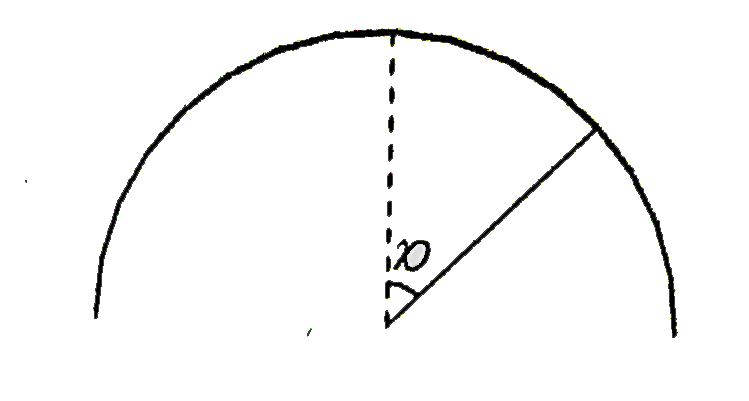
View SolutionAn insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by

View Solution
