A block of metal is lying on the floor of a bus. The maximum acceleration which can be given to the bus so that the block may remain at rest, will be -
μg
μ/g
μ2g
μg2
To solve the problem of determining the maximum acceleration that can be given to the bus so that the block remains at rest, we can follow these steps:
1. Identify the Forces Acting on the Block:
- The block experiences two main forces: the gravitational force (weight) acting downwards, Fg=mg, and the frictional force acting horizontally when the bus accelerates.
2. Understand the Frame of Reference:
- When the bus accelerates, the block may tend to slide due to inertia. To analyze this situation, we can consider the bus as a non-inertial frame of reference. In this frame, we introduce a pseudo force acting on the block in the opposite direction of the bus's acceleration.
3. Draw the Free Body Diagram (FBD):
- In the FBD, we have:
- The weight of the block acting downwards: Fg=mg
- The normal force N acting upwards.
- The frictional force Ff acting opposite to the direction of acceleration of the bus.
- The pseudo force Fp=ma acting in the opposite direction of the bus's acceleration.
4. Set Up the Equations:
- For the block to remain at rest relative to the bus, the net force acting on it must be zero. Thus, we can write:
- In the vertical direction: N=mg (normal force balances the weight)
- In the horizontal direction: Ff=ma (frictional force balances the pseudo force)
5. Express the Frictional Force:
- The maximum static frictional force can be expressed as:
Ff=μN=μmg
- Here, μ is the coefficient of static friction.
6. Equate the Forces:
- Setting the frictional force equal to the pseudo force gives us:
μmg=ma
7. Solve for Maximum Acceleration:
- Canceling m from both sides (assuming m≠0):
a=μg
- This equation tells us that the maximum acceleration a that can be given to the bus without the block sliding is μg.
Final Answer:
The maximum acceleration which can be given to the bus so that the block may remain at rest is a=μg.
---
- The block experiences two main forces: the gravitational force (weight) acting downwards, Fg=mg, and the frictional force acting horizontally when the bus accelerates.
- When the bus accelerates, the block may tend to slide due to inertia. To analyze this situation, we can consider the bus as a non-inertial frame of reference. In this frame, we introduce a pseudo force acting on the block in the opposite direction of the bus's acceleration.
- In the FBD, we have:
- The weight of the block acting downwards: Fg=mg
- The normal force N acting upwards.
- The frictional force Ff acting opposite to the direction of acceleration of the bus.
- The pseudo force Fp=ma acting in the opposite direction of the bus's acceleration.
- For the block to remain at rest relative to the bus, the net force acting on it must be zero. Thus, we can write:
- In the vertical direction: N=mg (normal force balances the weight)
- In the horizontal direction: Ff=ma (frictional force balances the pseudo force)
- The maximum static frictional force can be expressed as:
Ff=μN=μmg
- Here, μ is the coefficient of static friction.
- Setting the frictional force equal to the pseudo force gives us:
μmg=ma
- Canceling m from both sides (assuming m≠0):
a=μg
- This equation tells us that the maximum acceleration a that can be given to the bus without the block sliding is μg.
The maximum acceleration which can be given to the bus so that the block may remain at rest is a=μg.
Topper's Solved these Questions
Similar Questions
A block of mass 1.0 kg rests on a wedge of angle θ. The acceleration which should be given to the wedge so that the block falls freely is :
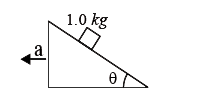 View Solution
View SolutionA block of mass m is placed on the rough incline of a wedge of mass M and inclination α to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is μ.
View Solution
Knowledge Check
- Question 1 - Select One
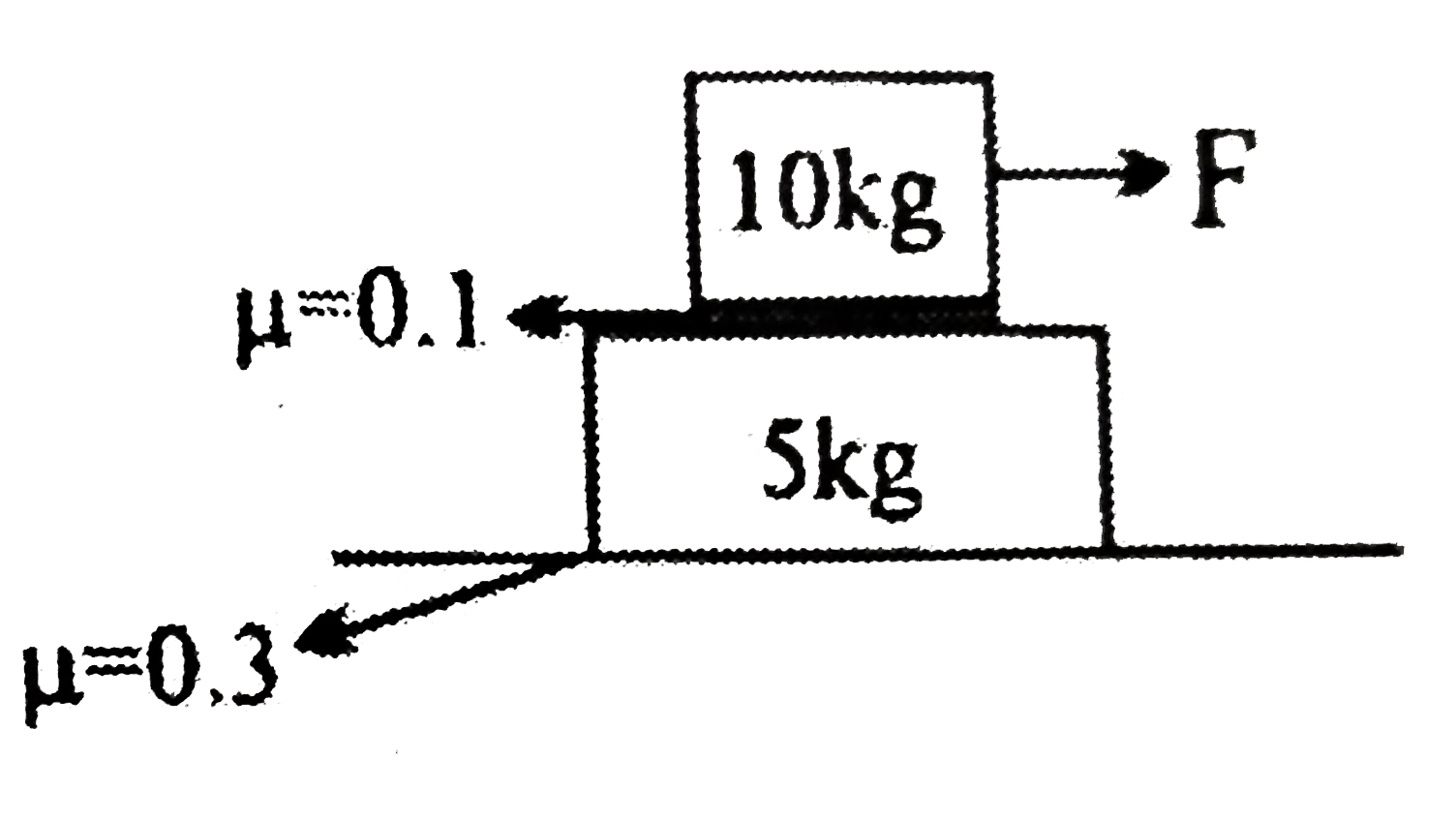
The maximum acceleration of 5 of kg block is :-A1m/s2B3m/s2C0DNone - Question 2 - Select One
A cylinder of mass m rests on a supporting block as shown. If β=60∘ and θ=30∘, calculate the maximum acceleration 'a' which the block may be given up the incline so that the cylinder does not lose contact at B. Neglect friction anywhere).
 Ag/2BgCg/3Dg/4
Ag/2BgCg/3Dg/4 - Question 3 - Select One
Figure shows a block kept on a rough inclined plane. The maximum external force along the plane downwards for which the block remains at rest is 1N while the maximum external force along the incline upwards for which the block is rest is 7N. The coefficient of static friction μ is
 A√32B1√6C√3D43√3
A√32B1√6C√3D43√3
Find minimum μ so that the blocks remain stationary.
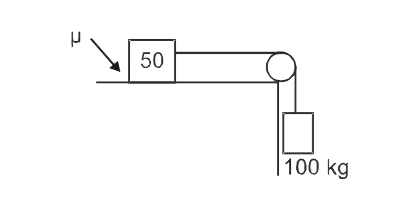 View Solution
View SolutionFind out acceleration of the block. Initially the block is at rest.
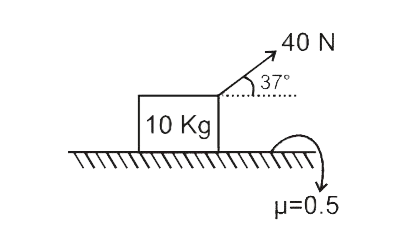 View Solution
View SolutionFind out acceleration of the block. Initially the block is at rest.
 View Solution
View SolutionFind acceleration of block. Initially the block is at rest.
 View Solution
View SolutionA block is lying static on the floor. The maximum value of static fictional force on the block is 10 N. If a horizontal force of 6 N is applied to the block,what will be the frictional force on the block?
View Solution

