A 2 kg body and a 3 kg body are moving along the x-axis. At a particular instant the 2 kg body has a velocity of 3ms−1 and the 3 kg body has the velocity of 2ms−1. The velocity of the centre of mass at that instant is
5ms−1
1ms−1
0
None of these
To find the velocity of the center of mass of the two bodies, we can use the formula for the velocity of the center of mass (V_cm):
Vcm=m1u1+m2u2m1+m2
Where:
- m1 = mass of the first body (2 kg)
- u1 = velocity of the first body (3 m/s)
- m2 = mass of the second body (3 kg)
- u2 = velocity of the second body (2 m/s)
1. Identify the masses and velocities:
- m1=2kg
- u1=3m/s
- m2=3kg
- u2=2m/s
2. Substitute the values into the formula:
Vcm=(2kg×3m/s)+(3kg×2m/s)2kg+3kg
3. Calculate the numerator:
=(6kg m/s)+(6kg m/s)5kg
=12kg m/s5kg
4. Calculate the velocity of the center of mass:
Vcm=125m/s=2.4m/s
Final Answer:
The velocity of the center of mass at that instant is 2.4m/s.
- m1 = mass of the first body (2 kg)
- u1 = velocity of the first body (3 m/s)
- m2 = mass of the second body (3 kg)
- u2 = velocity of the second body (2 m/s)
- m1=2kg
- u1=3m/s
- m2=3kg
- u2=2m/s
Vcm=(2kg×3m/s)+(3kg×2m/s)2kg+3kg
=(6kg m/s)+(6kg m/s)5kg
=12kg m/s5kg
Vcm=125m/s=2.4m/s
The velocity of the center of mass at that instant is 2.4m/s.
Topper's Solved these Questions
Similar Questions
Two bodies of masses 3 kg and 4 kg are moving along X axis. At a time t, the bodics are at a distance of 2 m and 3 m from the origin and has velocities of 2ms−1and−3ms−1. Calculate the position and velocity of centre of mass. What will be the total momentum of the system?
View SolutionCalculate the net force acting on a body of mass 10 kg moving with a unifrom velocity of 2ms−1 .
View Solution
Knowledge Check
A body of mass 20 kg is moving with a velocity of 2v and another body of mass 10 kg is moving with velocity V along same direction. The velocity of their centre of mass is
A5v/3B2v/3CvDZeroA bomb of mass 9kg explodes into two pieces of masses 3 kg and 6kg. The velocity of 3kg mass is 16ms−1. The velocity of 6kg mass is
A4ms−1B8ms−1C16ms−1D32ms−1Two bodies of masses 5kg and 3kg are moving towards each other with 2ms−1 and 4ms−1 respectively. Then velocity of centre of mass is
A0.25ms−1 towards 3kgB0.5ms−1 towards 5kgC0.25ms−1 towards5kgD0.5ms−1 towards 3kg
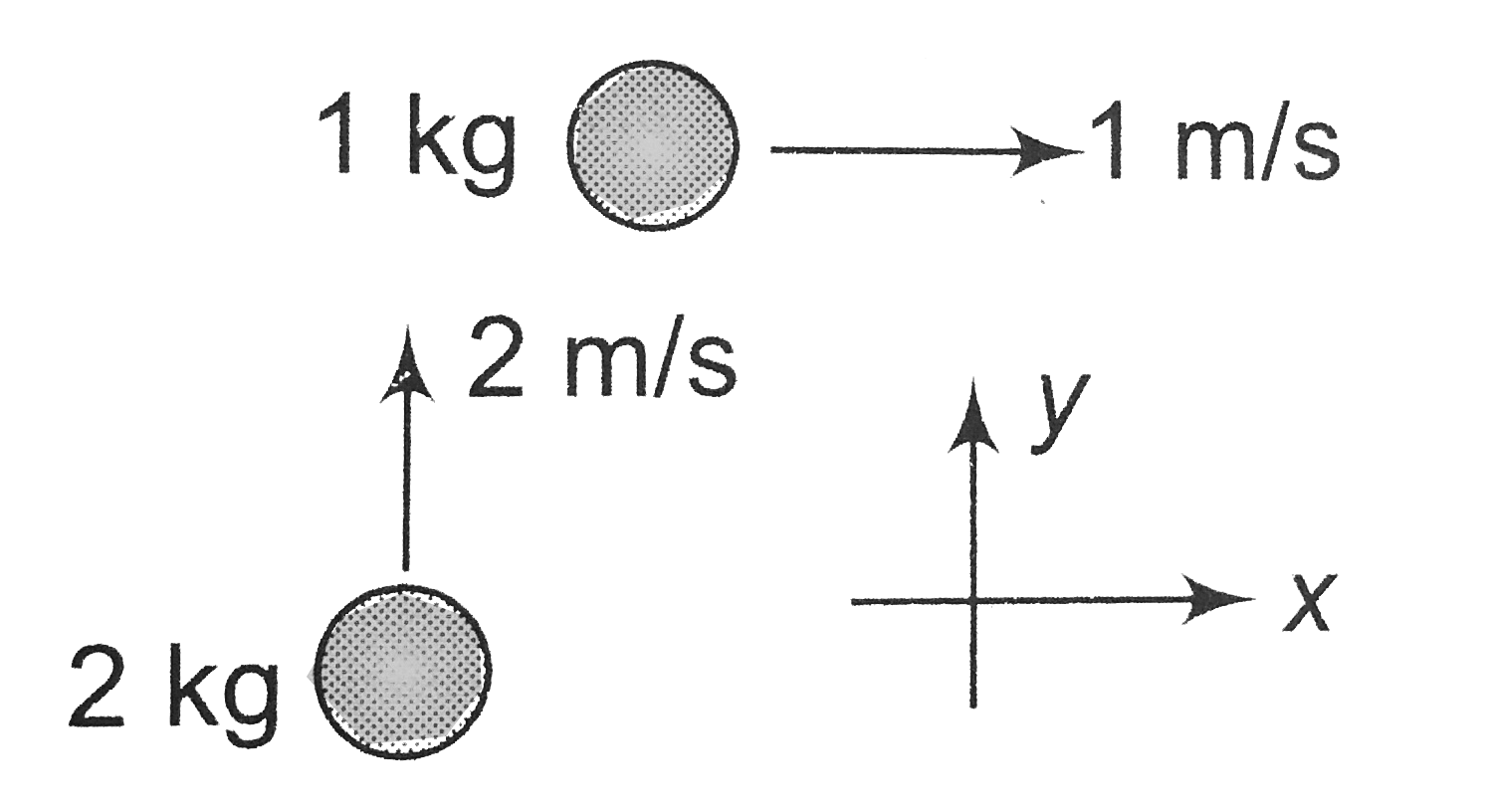
Two bodies of masses 1kgand2kg are moving in two perpendicular direction with velocities 1m/sand2m/s as shown in figure. The velocity of the centre of mass (in magnitide) of the system will be :
View SolutionA body of mass 10kg moving with a velocity of 5ms−1 hits a body of 1gm at rest. The velocity of the second body after collision. Assuming it to be perfectly elastic is
View SolutionThe velocity of 2 kg body is changed from (4ˆi+3ˆj)ms−1 to 6ms−1. The work done on the body is
View SolutionA body A of mass 5kg is moving along the x-axis with a velocity 2m/s. Another body (B) of mass 10 kg is moving along the y-axis with a velocity √3m/s. They collide at the origin and stick together. What is the final velocity of the combined mass?
View SolutionEscape velocity of a body 1kg mass on a planet is 100ms−1. Gravitational potential energy of the body at that planet is
View Solution
