A copper wire of diameter 1.6 mm carries a current of 20A. Find the maximum magnitude of the magnetic field (vec B)due to this current.
To find the maximum magnitude of the magnetic field (B) due to a current-carrying copper wire, we can use the formula for the magnetic field around a long straight conductor:
B=μ0I2πd
Where:
- B is the magnetic field,
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current in amperes (A),
- d is the distance from the center of the wire to the point where the magnetic field is being calculated.
1. Identify the given values:
- Diameter of the wire, D=1.6mm=1.6×10−3m
- Current, I=20A
2. Calculate the radius of the wire:
- The radius r is half of the diameter:
r=D2=1.6×10−32=0.8×10−3m
3. Determine the distance d:
- For maximum magnetic field, we calculate B at the surface of the wire, which means d=r.
4. Substitute the values into the magnetic field formula:
B=μ0I2πr
Substituting μ0=4π×10−7T m/A, I=20A, and r=0.8×10−3m:
B=4π×10−7×202π×(0.8×10−3)
5. Simplify the equation:
- The π terms cancel out:
B=4×10−7×202×(0.8×10−3)
B=80×10−71.6×10−3
6. Calculate the magnetic field:
- Performing the division:
B=80×10−7÷1.6×10−3=80÷1.6×10−4=50×10−4=5×10−3T
7. Convert to milliTesla:
B=5mT
Final Answer:
The maximum magnitude of the magnetic field due to the current in the copper wire is 5milliTesla.
- B is the magnetic field,
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current in amperes (A),
- d is the distance from the center of the wire to the point where the magnetic field is being calculated.
- Diameter of the wire, D=1.6mm=1.6×10−3m
- Current, I=20A
- The radius r is half of the diameter:
r=D2=1.6×10−32=0.8×10−3m
- For maximum magnetic field, we calculate B at the surface of the wire, which means d=r.
B=μ0I2πr
Substituting μ0=4π×10−7T m/A, I=20A, and r=0.8×10−3m:
B=4π×10−7×202π×(0.8×10−3)
- The π terms cancel out:
B=4×10−7×202×(0.8×10−3)
B=80×10−71.6×10−3
- Performing the division:
B=80×10−7÷1.6×10−3=80÷1.6×10−4=50×10−4=5×10−3T
B=5mT
The maximum magnitude of the magnetic field due to the current in the copper wire is 5milliTesla.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
A silver wire has resistivity ρ=1.62×10−8Ωm and cross-sectional area 10.0mm2. The current in the wire is uniform and changing at the rate of 4000A/s, when the current is 200A. (a) What is the magnitude of the electric field in the wire when the current in the wire is 200A? (b) What is the displacement current in the wire at that time (c) What is the ration of the magnitude of the magnetic field due to the displacement current to that due to the current at a distance r from the wire?
View SolutionA long straight wire carries a current of 35 A. What is the magnitude of the field →B at a point 20 cm from the wire?
View Solution
Knowledge Check
Figure shows a straight wire of length l carrying a current i. Find the magnitude of magnetic field produced by the current at point P.
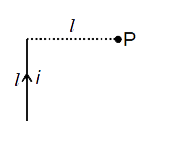 A√2μ0i3π1B√2μ0i8π1Cμ0i2π1D√2μ0iπl
A√2μ0i3π1B√2μ0i8π1Cμ0i2π1D√2μ0iπlA wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
Aπμ0ILBμ0I2LC2πμ0ILDμ0I2πLA straight wilre of diameter 0.5mm carrying a current 2A is replaced by another wire of diameter 1mm carrying the same current. The strength of magnetic field at a distance 2m away from the centre is
Ahalf of the previous valueBtwice of the previous valueCunchangedDquarter of its previous value
A long straight wire carries a current of 35 A. What is the magnitude of the field →B at a point 20 cm from the wire?
View SolutionDraw the magnetic field lines due to a straight wire carrying current.
View SolutionA solenoid consists of 250 turns of wire and has a length of 20 cm. Calculate the magnitude of the magnetic field inside the solenoid if it carries a current of 1A.
View SolutionA straight wire of diameter 0.5mm carrying a current of 1A is replaced by another wire of 1mm diameter carrying the same current. The strength of magnetic field far away is
View SolutionA straight wire of diameter 0.4 mm carrying a current of 2A is replaced by another wire of 0.8 mm diameter and carrying the same current. The magnetic field at the same distance from the wire is
View Solution
