A sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The electric field inside the sphere is
3Q∈0R2[13(rR)−14(rR)2]
12Q2R3[13(rR)−14(rR)2]
120Q5∈0R2[14(rR)−13(rR)2]
12R2Q[13(rR)−14(rR)2]
Step by step video & image solution for A sphere of radius R contains charge density rho(r )=A (R-r ), for 0 lt r lt R. The total electric charge inside the sphere is Q. The electric field inside the sphere is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The electric outside the sphere is (k=14π∈0)View SolutionA sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The value of A in terms of Q and R isView Solution
Knowledge Check
- Question 1 - Select One
An insulating solid sphere of radius R has a uniformaly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: Wgen a charge 'q' is taken from the centre to the surface of the sphere, its potential energy charges by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0AStatement-1 is true, Statement-2 is true and Statement-2 is the correct explanation of Statement-1BStatement-1 is true, Statement-2 is true and Statement-2 is not the correct explanation of Statement-1CStatement-1 is true, Statement-2 is falseDStatement-1 is false, Statement-2 is true - Question 2 - Select One
The electric field due to point charged at a distance R form it is E. if the same charge is placed on a metallic sphere of Radius R, the electric field on the surface of the sphere will be
AzeroB10 VCmore thanDnone of these - Question 3 - Select One
A system consists of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr , where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
Aα2ε0B2αε0C2παR2DNone of these
A solid sphere of radius R is charged with volume charge density p=Krn , where K and n are constants and r is the distance from its centre. If electric field inside the sphere at distance r is proportional to r4 ,then find the value of n.
View SolutionA solid ball of radius R has a charge density ρ given by ρ=ρ0(1−rR)for0≤r≤R The electric field outside the ball is :
View SolutionA solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionA solid sphere of radius R has a charge +2Q. A hollow spherical concentric with the first sphere that has net charge -Q.
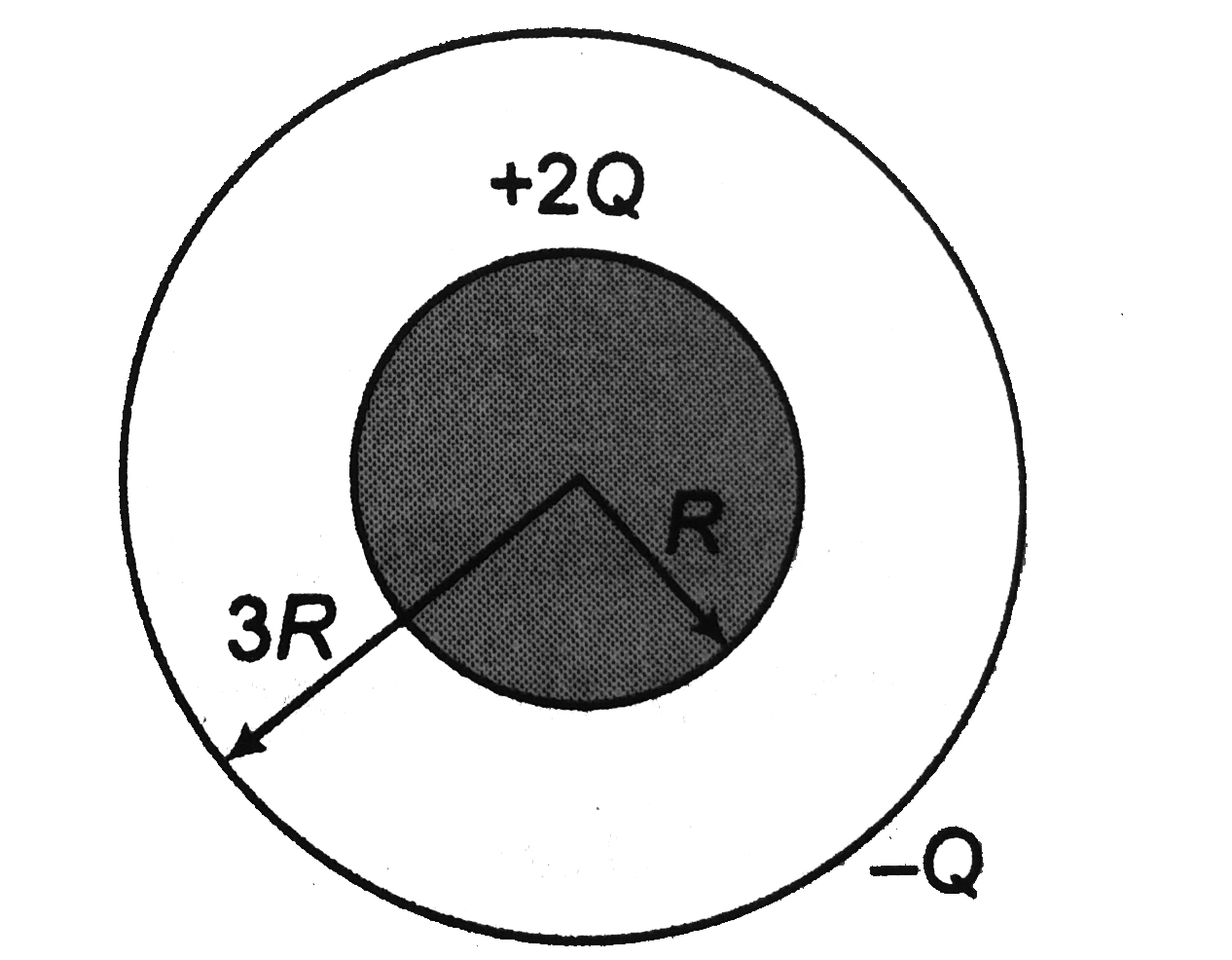
(a) Find the electric field between the spheres at a distance r from the centre of the inner sphere. [R<r<3R]
(b) Calculate the potential difference between the spheres.
(c) What would be the final distribution of charges, if a conducting wire joins the spheres?
(d) Instead of (c), if the inner sphere is earthed, what is the charge on it?View SolutionA Sphere of radius R0 carries a volume charge density proportional to the distance (x) from the origin, ρ=αx where α is a positive constant. (a) Calculate the total charge in the sphere of radius R0. (b) The sphere is shaved off so as to reduce its radius. What should be the radius (R) of the remaining sphere so that it contains half the charge of the original sphere? (c) Find the electric field at a point inside the sphere at a distance r lt R. Give your answer for original sphere of radius R0 as well as for the smaller sphere of radius R that was left after shaving off the original sphere.
View Solution

