A particle P will be in equilibrium inside a hemispherical bowl of radius 0.5 m at a height 0.2 m from the bottom when the bowl is rotated at an angular speed ( g = 10 m/sec2)

A

$10 / \sqrt{3} r a d / sec$

B

$10 \sqrt{r} a d / sec$

C

$10 r a d / sec$

D

$\sqrt{20} r a d / sec$

Text Solution

Verified by Experts

The correct Answer is:A

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

BOOK - MOTIONCHAPTER - SHM-WAVE,GRAVITATION,FLUID,HEATEXERCISE - EXERCISE
109videos
SHM-WAVE,GRAVITATION,FLUID,HEAT

Similar Questions

Knowledge Check

Question 1 - Select One
A particle P will be in equilibrium inside a hemispherical bowl of radius 0.5 m at a height 0.2 m from the bottom when the bowl is rotated at an angular speed $(g = 10 m / {sec}^{2})$

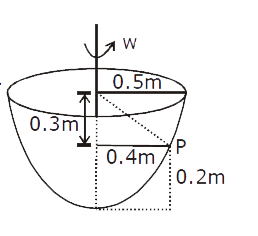A $10 / \sqrt{3}$ rad/sec
B $10 \sqrt{3}$ rad/sec
C10 rad/sec
D $\sqrt{20}$ rad/sec
Question 2 - Select One

A small mass of 10 g lies in a hemispherical bowl of radius 0.5 m at a height of 0.1 m from the bottom of the bowl. The mass will be in equilibrius if the bowl rotates at an
A $\frac{10}{\sqrt{3}} \frac{r a d}{s}$
B $10 \sqrt{3} \frac{r a d}{s}$
C $5 \frac{r a d}{s}$
Dnone of these
Question 3 - Select One
A ball is moving to and fro about the lowest point A of a smooth hemispherical bowl. If it is able to rise up to a height of 20 cm on either side of A , its speed at A must be (Take $= 10 m / s$ , mass of the body 5 g )
A $0.2 m / s$
B $2 m / s$
C $4 m / s$
D $4.5 m s$

MOTION-MECHANICS-EXERCISE

Home
Ask Doubt
Profile