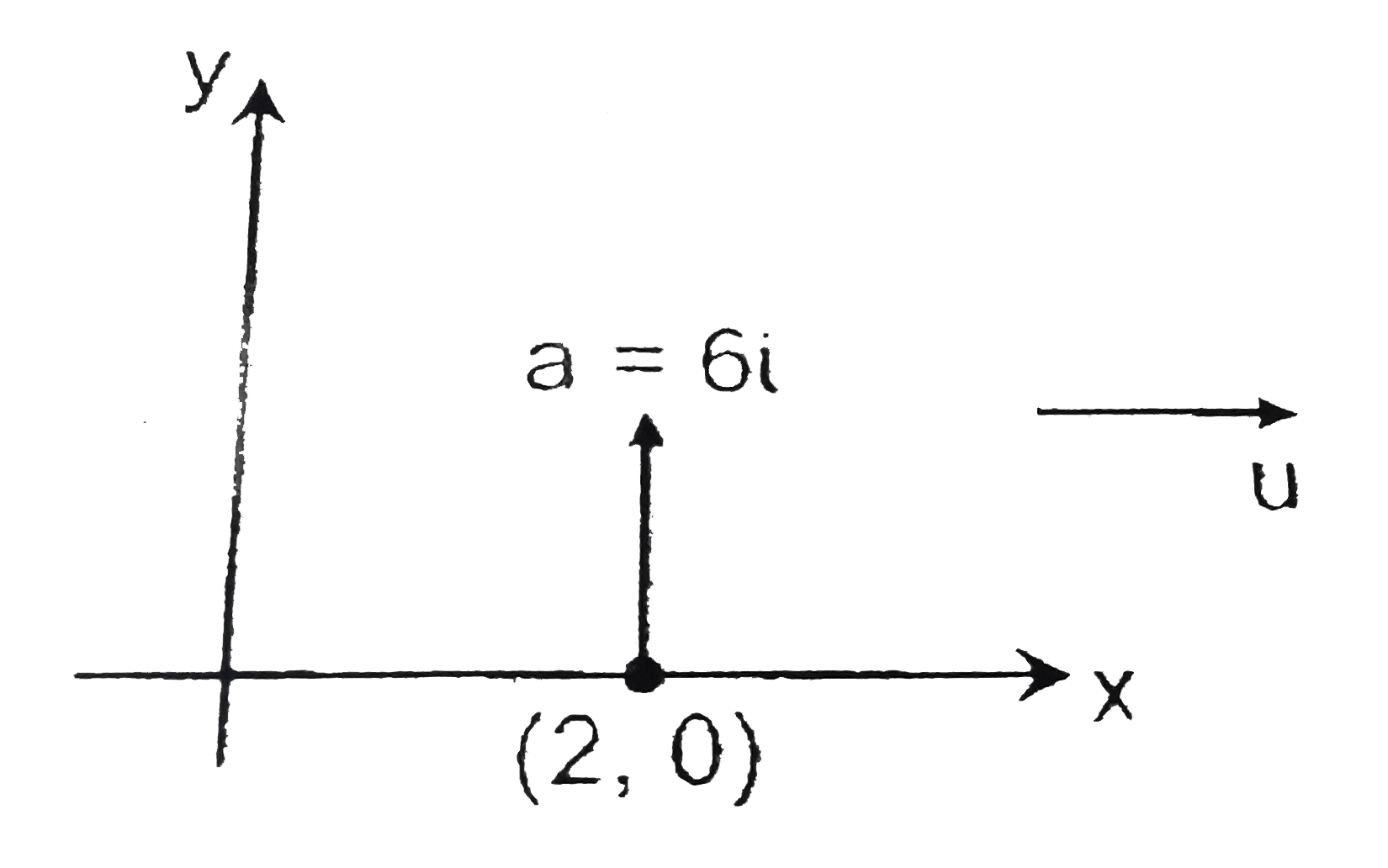
A boat starting from rest aims perpendicular to the river with an acce

Topper's Solved these Questions

BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30videos
TEST PAPERS
BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30videos
TEST PAPERS
BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107videos
TEST PAPERS
BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13videos
SIMPLE HARMONIC MOTION
BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127videos
TEST SERIES

Knowledge Check

Question 1 - Select One
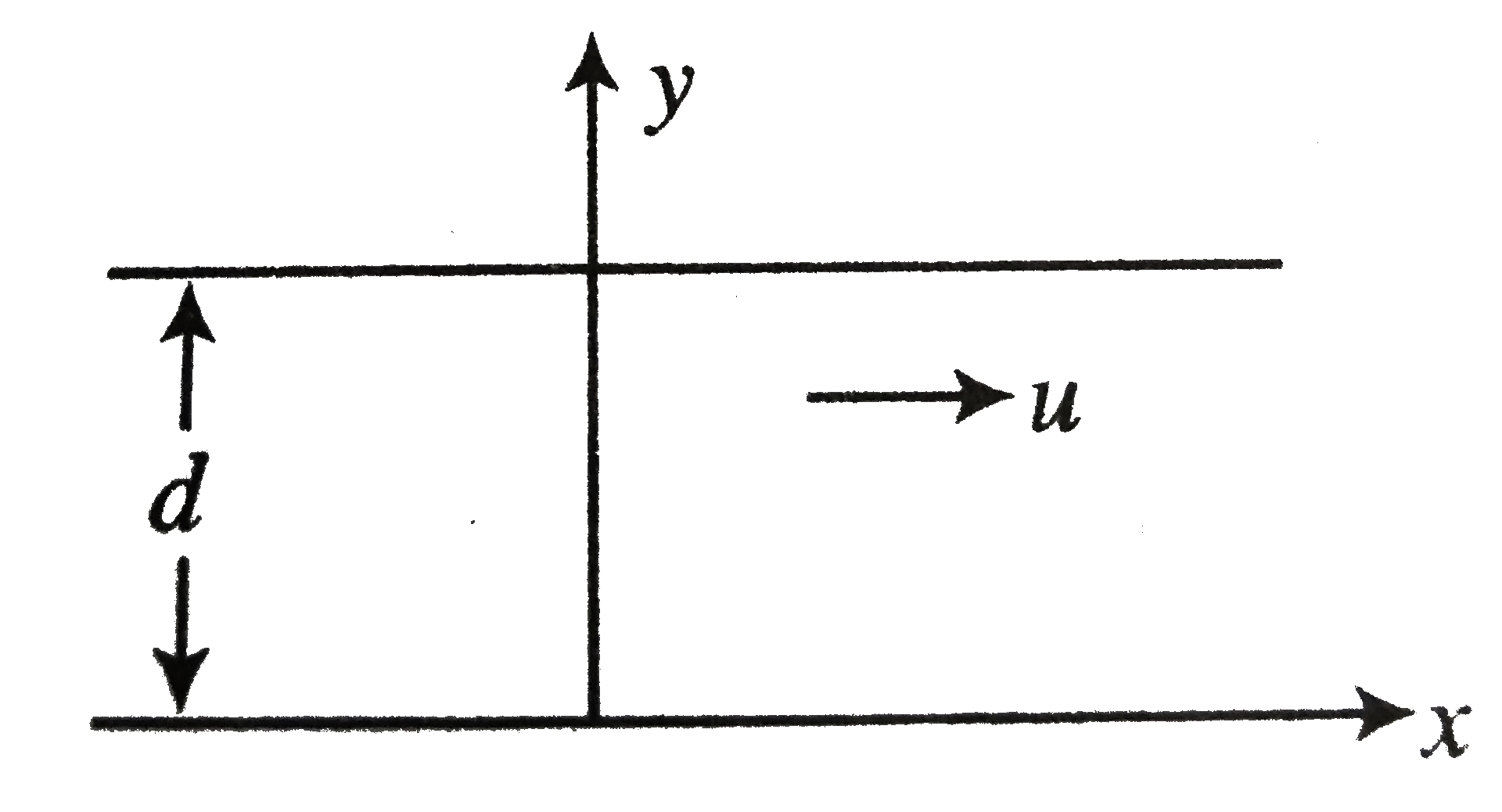
We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

${\to v}_{b o a t} = {\to v}_{b o a t, w a t e r} + {\to v}_{w a t e r}$ .
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
A $u {(\frac{3 d}{5})}^{1 / 3}$
B $u {(\frac{3 d}{5})}^{1 / 3}$ + 1
C $u {(\frac{6 d}{5})}^{1 / 3}$
DNone of these
Question 2 - Select One
We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

${\to v}_{b o a t} = {\to v}_{b o a t, w a t e r} + {\to v}_{w a t e r}$ .
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
A ${(3 d / 5)}^{1 / 3}$
B ${(6 d / 5)}^{1 / 3}$
C ${(6 d / 5)}^{1 / 2}$
D ${(2 d / 3)}^{1 / 3}$
Question 3 - Select One
We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

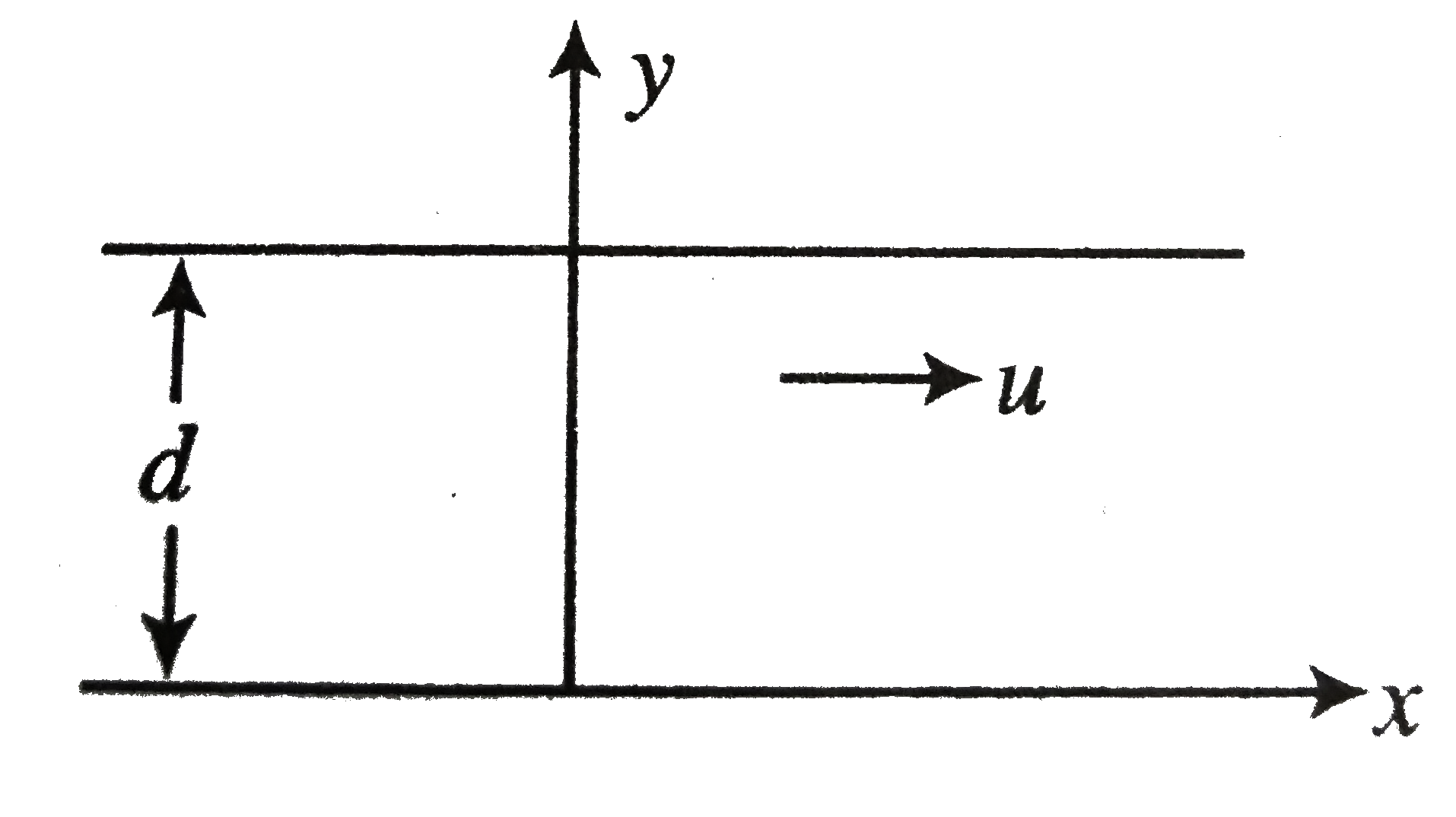
${\to v}_{b o a t} = {\to v}_{b o a t, w a t e r} + {\to v}_{w a t e r}$ .
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
A $x - 1 = u {(\frac{3 y}{5})}^{1 / 3}$
B $x = u {(\frac{6 y}{5})}^{1 / 3}$
C $x = 1 = u {(\frac{6 y}{5})}^{1 / 3}$
DNone of these

A boat starting from rest aims perpendicular to the river with an acceleration of $a = 6 t$
(where $t =$ time) the boat starts from $(2, 0)$ of the coordinate system. Find equation of trajectory. Given velocity of river $= u$ .

The correct Answer is:B

$\frac{d v}{d t} = 6 t \Rightarrow v = \frac{6 t^{2}}{2} = 3 t^{2}$
$\frac{d y}{d t} = 3 t^{2}$
$y = t^{3}$
${(y)}^{\frac{1}{3}} = \frac{(x - 2)}{u}$
$u y^{\frac{1}{3}} = (x - 2)$

Topper's Solved these Questions

Similar Questions

Knowledge Check

RESONANCE-TEST PAPERS-Physics

A boat starting from rest aims perpendicular to the river with an acceleration of a=6t (where t= time) the boat starts from (2,0) of the coordinate system. Find equation of trajectory. Given velocity of river =u.

The correct Answer is:B

dvdt=6t⇒v=6t22=3t2 dydt=3t2 y=t3 (y)13=(x−2)u uy13=(x−2)

Topper's Solved these Questions

Similar Questions

Knowledge Check

RESONANCE-TEST PAPERS-Physics

A boat starting from rest aims perpendicular to the river with an acceleration of $a = 6 t$
(where $t =$ time) the boat starts from $(2, 0)$ of the coordinate system. Find equation of trajectory. Given velocity of river $= u$ .

$\frac{d v}{d t} = 6 t \Rightarrow v = \frac{6 t^{2}}{2} = 3 t^{2}$
$\frac{d y}{d t} = 3 t^{2}$
$y = t^{3}$
${(y)}^{\frac{1}{3}} = \frac{(x - 2)}{u}$
$u y^{\frac{1}{3}} = (x - 2)$