A particle starts from rest with a time varying acceleration a=(2t−4). Here t is in second and a in m/s2
The velocity time graph of the particle is
parabola passing through origin
straight line not passing through origin
parabola not passing through origin
straight line passing through origin
The correct Answer is:A
Step by step video, text & image solution for A particle starts from rest with a time varying acceleration a=(2t-4). Here t is in second and a in m//s^(2) The velocity time graph of the particle is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - MATCH THE COLUMN10videos
KINEMATICS 1
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE27videos
KINEMATICS 1
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE11videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
Similar Questions
A particle starts from rest at t=0 and undergoes an acceleration as shown in figure.
Draw the velocity-time graph of the motion of the particle during the interval from zero to 4 second.
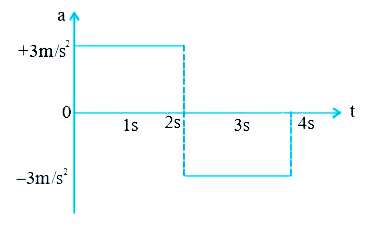 View Solution
View SolutionA particle starts from rest, moving in a straight line with a time varying acceleration (inm/s2):a=30−152√t, where time is in seconds . The displacement of the particle in 4 seconds is .
View Solution
Knowledge Check
- Question 1 - Select One
A particle starts from rest with a time varying acceleration a=(2t−4). Here t is in second and a in m/s2
Maximum velocity of particle in negative direction is at t=…………… secondA3B4C2D1 - Question 2 - Select One
A particle starts from rest with a time varying acceleration a=(2t−4). Here t is in second and a in m/s2
Particle comes to rest after a time t=………… secondA1B4C3D2 - Question 3 - Select One
Velocity of a particle of mass 2kg varies with time t according to the equation →v=(2tˆi+4ˆj)m/s. Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
A2ˆim/sB4ˆim/sC8ˆim/sD6ˆim/s
Velocity of particle of mass 2kg varies with time t accoridng to the equation →v=(2tˆi+4ˆj)ms−1. Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
View SolutionA particle starts from rest. Its acceleration at time t=0 is 5m/s2 which varies with time as shown in the figure. The maximum speed of the particle will be
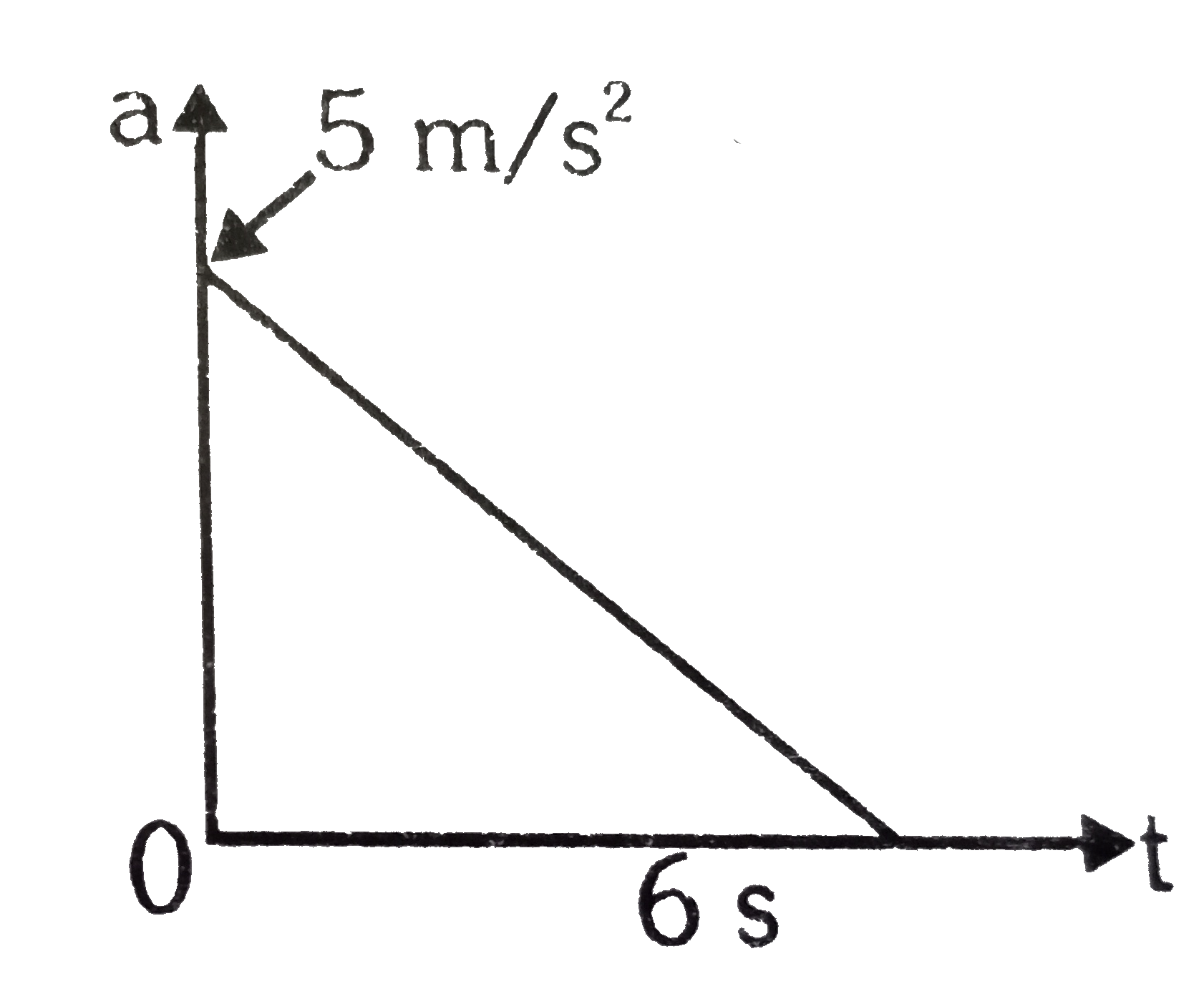 View Solution
View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = 1 s will be :View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the magnitude of displacement (in meters) by the particle from time t = 0 to t = t will be :View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = t will be :View Solution

