
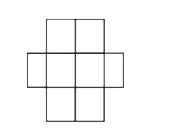
Six X's are to be placed in boxes of the figure such that each row contains at least one X, In how many different ways can this be done?
28
27
26
29
The correct Answer is:C
In all we have 9 squares in which 6 X have to be placed and it can be done in .^(8)C_(6)=28ways<br>Buthis∈cludesthepossibilitytˆeitherthe⊤orlowestrowsdoes¬haveanyX.Sincewewanteachrowμsthaveat≤∗o≠Xthesetwopossibilitiesare→beexcluded.Hence,requriedνmberofways=28-2=26
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS SEC - 11videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS9videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY37videos
TEST PAPER
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - MATHEMATICS131videos
TEST SERIES
Similar Questions
Six X ' s have to be placed in thesquares of the figure below, such that each rowcontains atleast one X. In how many different wayscan this be done?
View SolutionSix X 's have to be placed in the squares of the figure below, such that each row contains atleast one X. in how many different ways can this be done?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Six X ' s have to be placed in thesquares of the figure below, such that each rowcontains atleast one X. In how many different wayscan this be done?
A27B28C26D35 - Question 2 - Select One
Six X have to be placed in the squares of Fig. 6.6 such that each row contain at least one X. The number of ways in which this can be done is
 A25B26C27D30
A25B26C27D30 - Question 3 - Select One
4 boys and three girls are to be seated in a row in such way that no two boys sit adjacent to each other in how many different ways can it be done?
A5040B30C144D72
Six X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:
 View Solution
View SolutionSix Ps have to be placed in the squares of the diagram given below such that each column contains at least one P. In how many ways this can be done?
 View Solution
View SolutionSix X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:
 View Solution
View SolutionFive balls of different color are to be placed in three boxes of different size. Each box can hold all five. In how many different ways can we placed the balls so that no box remains empty?
View SolutionA select group of 4 is to be formed from 8 men and 6 women in such a way that the group must have at least 1 woman. In how many different ways can it be done? (a) 364 (b) 728 (c) 931 (d) 1001 (e) None of these
View Solution

