
A particle of mass m is projected up from the bottom of an inclined plane with initial velocity v0 at angle 45∘ with an inclined plane of inclination 30∘ as shown in figure. At the same time a small block of same mass m is released from rest at a height h, the particle hits the block at some point on the inclined plane. Neglect friction at inclined.
Q. The value of height h is
v20g
√3v20g
2v20√3g
v20√3g
The correct Answer is:D
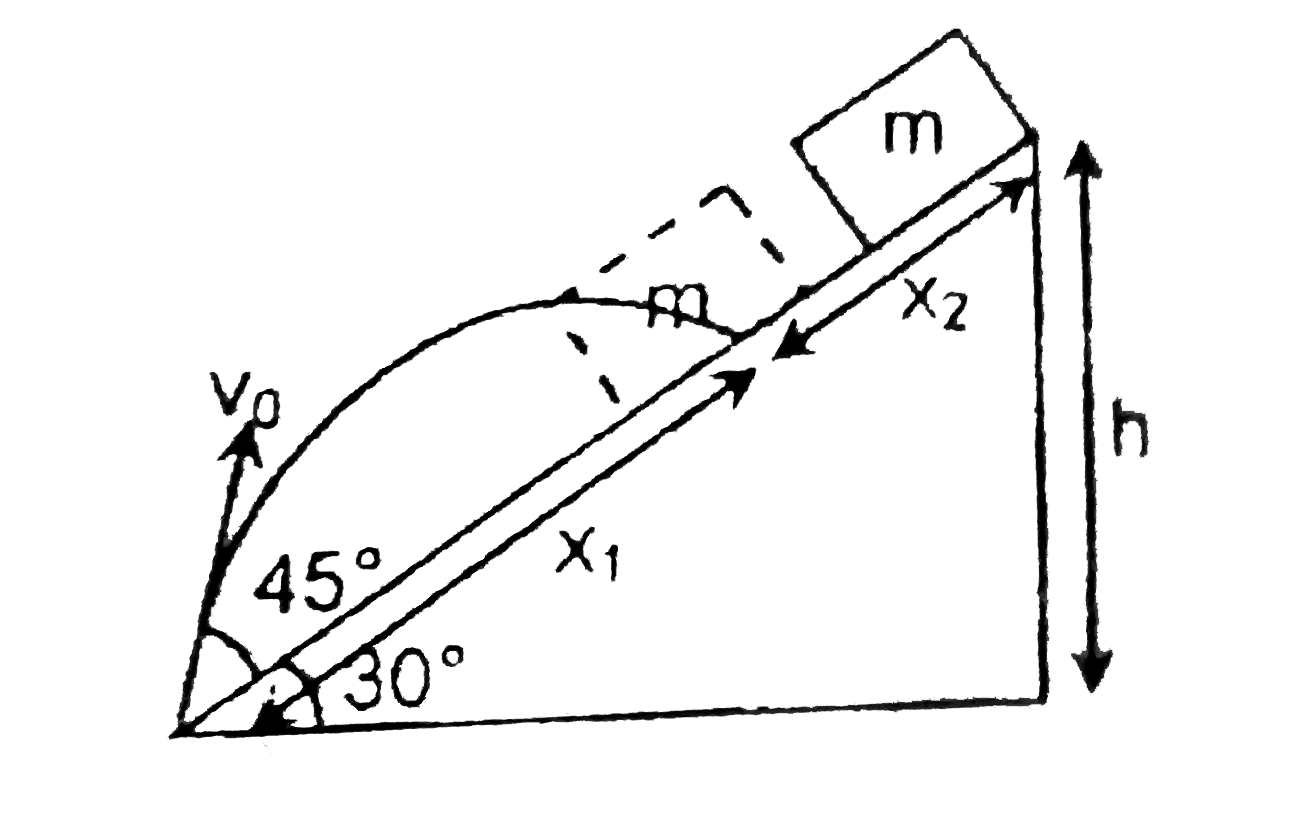
T=2V0sin45∘2gcos30=2√2V0√3g
since x1+x2=2h
⇒(V0√22√2v0√3g−12gsin30∘×8v203g2)+(12g28v203g)=2h
h=v20√3g
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A block of mass m is released from the top of fixed inclined smooth plane. if theta is the angle of inclination then vertical accelertion of block is
View SolutionA ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
View Solution
Knowledge Check

A particle of mass m is projected up from the bottom of an inclined plane with initial velocity v0 at angle 45∘ with an inclined plane of inclination 30∘ as shown in figure. At the same time a small block of same mass m is released from rest at a height h, the particle hits the block at some point on the inclined plane. Neglect friction at inclined.
Q. If the particlee stick to the block after collision the velocity of block parallel tot he inclined plane just after collision will be (take g=10ms2Av0√2Bv02Cv02√2(1−4√3)Dv02√2(1+4√3)A particle of mass m is projected up from the bottom of an inclined plane with initial velocity v0 at angle 45∘ with an inclined plane of inclineation 30∘ as shown in figure. At the same time a small block of same mass m is released from rest at a height h. The particle hits the block at some point on inclined plane.
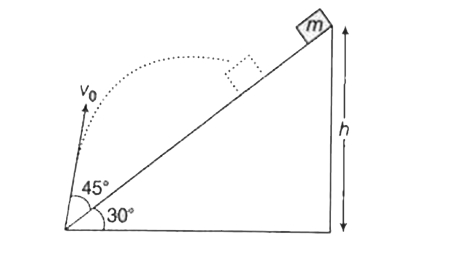
The value of height h isAv20gB√3v20gC2v20√3gDv20√3gA particle of mass m is projected up from the bottom of an inclined plane with initial velocity v0 at angle 45∘ with an inclined plane of inclineation 30∘ as shown in figure. At the same time a small block of same mass m is released from rest at a height h. The particle hits the block at some point on inclined plane.
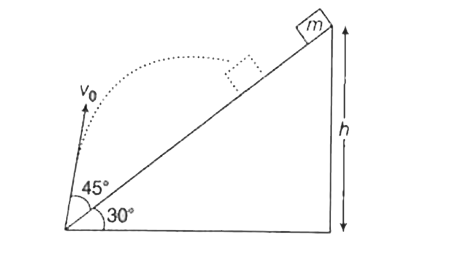
If the particle sticks to the block after collision, the velocity of block parallel to the inclined plane just after collision will be (take g=10m/s2)Av0√2Bv02Cv02√2(1−4√3)Dv02√2(1+4√3)
A block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View SolutionA particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is β. It strikes. the plane at right angles if
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View Solution
