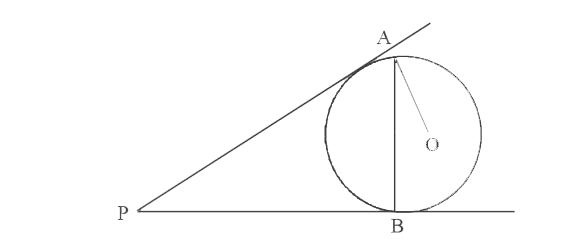
In the figure, a tangent PT and 2 line signs PBA is drawn to a circle with center O. If $O L ⊥ A B$ . Prove that the $P A \times P B = P T^{2}$ .

Video Solution

|

Answer

Step by step video & image solution for In the figure, a tangent PT and 2 line signs PBA is drawn to a circle with center O. If OL _|_AB. Prove that the PA xx PB=PT^2. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS REAL NUMBERS

Similar Questions

In the figure, a tangent PT and 2 line signs PBA is drawn to a circle with center O. If $O L ⊥ A B$ . Prove that the $P A \times P B = P T^{2}$ .
View Solution
In the given Fig. 5, from an external point P, a tangent PT and a secant PAB is drawn to a circle with centre 0. ON is perpendicular on the chord AB. Prove that $P A . P B = P T^{2}$ ?.

View Solution
In the given figure, from an external point P, a tangent PT and a line segment PAB is drawn to a circle with centre O. ON is perpendicular on the chord AB. Prove that (i) $P A . P B = P N^{2} - A N^{2}$ (ii) $P N^{2} - A N^{2} = O P^{2} - O T^{2}$
View Solution
Two tangent segments $P A$ and $P B$ are drawn to a circle with centre $O$ such that $∠ A P B = 120 o$ . Prove that $O P = 2 A P$ .
View Solution
As shown in the given figure, from an external point P, a tangent PT and a line segment PAB are drawn to a circle with centre O. ON is perpendicular on the chord AB, Prove that
$P A . P B = P N^{2} - A N^{2}$
View Solution
In Figure, two tangents $A B a n d A C$ are drawn to a circle with centre $O$ such that $∠ B A C = 120^{0} .$ Prove that $O A = 2 A B$
View Solution
From a point P, two tangents PT and PS are drawn to a circle with center O.Such that $∠ S P T = 120^{\circ}$ . Prove that OP=2PS.
View Solution
Two tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that $∠ A P B = 2 ∠ O A B$

View Solution
From a point P, two tangents PT and PS are drawn to a circle with centre O such that $∠ S P T = 120^{\circ}$ Prove that OP = 2PS.
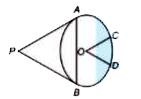
View Solution
In the given figure, from the point P two tangents PA and PB are drawn to a circle with centre O and radius 5cm. From the point O, OC and OD are drawn parallel to PA and PB respectively. If the length of the chord AB is 5cm, then what is the value of (in degrees) of $∠ C O D$ ?

View Solution

In the figure, a tangent PT and 2 line signs PBA is drawn to a circle with center O. If OL⊥AB. Prove that the PA×PB=PT2.

Similar Questions

Recommended Questions

In the figure, a tangent PT and 2 line signs PBA is drawn to a circle with center O. If $O L ⊥ A B$ . Prove that the $P A \times P B = P T^{2}$ .