A simple pendulum consisting of a ball of mass m tied to a thread of length l is made to swing on a circular arc of angle q in a vertical plane. At the end of this arc, another ball of mass m is placed at rest. The momentum transferred to this ball at rest by the swinging ball is
Zero
mθ√gl
mθl√lg
ml2π√lg
To solve the problem of momentum transfer from a swinging pendulum ball to a stationary ball, we can follow these steps:
Step 1: Understand the system
We have a simple pendulum with a ball of mass m swinging in a circular arc at an angle θ. At the end of this arc, we place another ball of mass m at rest.
Step 2: Analyze the position of the swinging ball
At the extreme position of the swing (the angle θ), the swinging ball momentarily comes to rest. This means that at this point, the velocity of the swinging ball is zero.
Step 3: Determine the momentum of the swinging ball
Momentum is defined as the product of mass and velocity. The momentum p of the swinging ball is given by:
p=m⋅v
Since the velocity v of the swinging ball at the extreme position is zero, we have:
p=m⋅0=0
Step 4: Consider the stationary ball
The stationary ball is at rest, which means its initial momentum is also zero. When the swinging ball reaches the extreme position and has zero velocity, it cannot transfer any momentum to the stationary ball.
Step 5: Conclusion on momentum transfer
Since the swinging ball has zero momentum at the moment it reaches the stationary ball, the momentum transferred to the stationary ball is also zero.
Thus, the final answer is:
Momentum transferred to the ball at rest=0
We have a simple pendulum with a ball of mass m swinging in a circular arc at an angle θ. At the end of this arc, we place another ball of mass m at rest.
At the extreme position of the swing (the angle θ), the swinging ball momentarily comes to rest. This means that at this point, the velocity of the swinging ball is zero.
Momentum is defined as the product of mass and velocity. The momentum p of the swinging ball is given by:
p=m⋅v
Since the velocity v of the swinging ball at the extreme position is zero, we have:
p=m⋅0=0
The stationary ball is at rest, which means its initial momentum is also zero. When the swinging ball reaches the extreme position and has zero velocity, it cannot transfer any momentum to the stationary ball.
Since the swinging ball has zero momentum at the moment it reaches the stationary ball, the momentum transferred to the stationary ball is also zero.
Momentum transferred to the ball at rest=0
Topper's Solved these Questions
Similar Questions
A simple pendulum of length l and with a bob of mass m moving alon a circular are of angle θ in a vertical plane. A sphere of mass m is placed at the end of the circular arc. What momentum will be given to the sphere by the moving bob?
View SolutionA simple pendulum consists of a ball of mass m connected to a string of length L. The ball is pulled aside so that the string makes an angle of 53∘ with the verticle and is released. Find the ratio of the minumum and the tension in the string.
View Solution
Knowledge Check
A ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
AMvBmvCMmM+mvDM2M+mvA ball of mass m1, collides elastically and head on with ball of mass m2 at rest. Then
AThe transfer of kinetic energy to the second ball is maximum when m1=m2BThe change of momentum of first ball is maximum, when m1<<m2.CThe velocity of the second ball is maximum, when m1>>m2.DNone of theseA simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is
 A(a) cos−1[Lcosα+lL+l]B(b) cos−1[Lcosα+lL−l]C(c) cos−1[Lcosα−1L−l]D(d) cos−1[Lcosα−1L+l]
A(a) cos−1[Lcosα+lL+l]B(b) cos−1[Lcosα+lL−l]C(c) cos−1[Lcosα−1L−l]D(d) cos−1[Lcosα−1L+l]
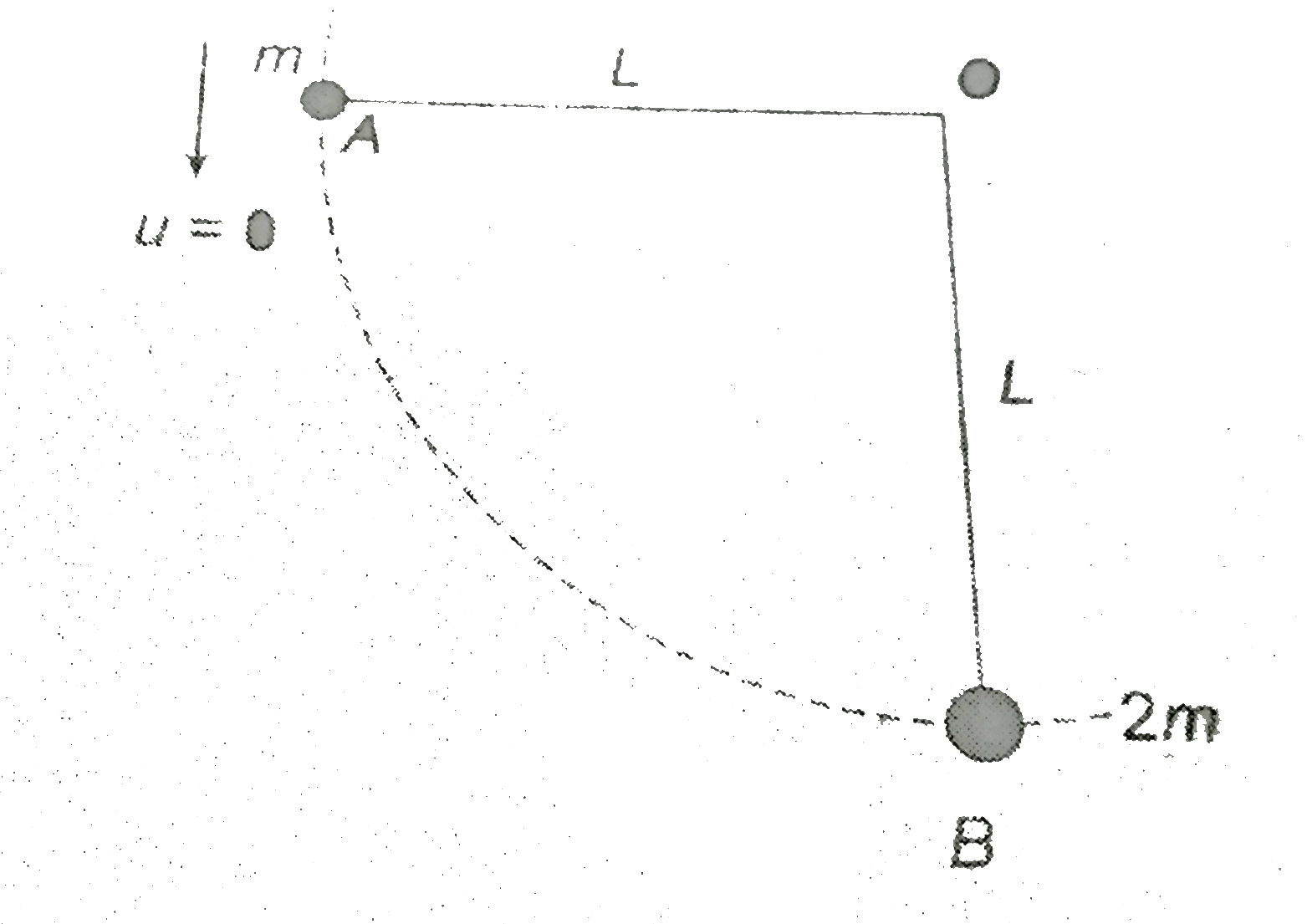
A ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
View SolutionTwo balls of mass m each are placed at the two vertices of an equilateral triangle. Another ball of mass 2m is placed at the third vertex of the triangle. Locate the centre of mass of the system.
View SolutionA simple pendulum of length l and consisting of a ball of mass m is released from a position making an angle θ=cos−1 (0.8) with the vertical and strikes at its lowest position a block of mass M resting on a rough horizontal plane. If the coefficient of kinetic friction between the plane and the block is 0.2 find
(a) How long the block will move along the plane, if the ball of the pendulum rebounds to an angle β=cos−1 (0.9)A
(b) The coefficient of restitution, use Mm=10 and 1= 1 m
View SolutionA ball of mass M is thrown vertically upwards. Another ball of mass 2M is thrown at an angle θ with the vertical. Both of them stay in air for the same period of time. The heights attained by the two are in the ratio
View Solution
A simple pendulum consists of a bob of mass m and a light string of length l as shown in the fig. another identical ball moving with the small velocity v0 collides with the pendulum's bob and sticks to it. For this new pendulum of mass 2 m, mark out the correct statements (s).
View Solution
