A random variable X has the following probability distribution: Values of X:0 1 2 3 4 5 6 7 8 P(x):a 3a 5a 7a 9a 11a 13a 15a 17a Determine: (i). The value of a (ii) P(X<3), P(X≥3), P(0<X<5)
To solve the problem step by step, we will follow the instructions provided in the question.
Step 1: Determine the value of a
The first step is to use the property of probability distributions, which states that the sum of all probabilities must equal 1.
The probabilities given are:
- P(X=0) = a
- P(X=1) = 3a
- P(X=2) = 5a
- P(X=3) = 7a
- P(X=4) = 9a
- P(X=5) = 11a
- P(X=6) = 13a
- P(X=7) = 15a
- P(X=8) = 17a
Now, we will sum these probabilities:
\(
P(X) = a + 3a + 5a + 7a + 9a + 11a + 13a + 15a + 17a
\)
Calculating the sum:
\(
= a(1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17)
\)
Calculating the sum of the coefficients:
\(
1 + 3 = 4
\)
\(
4 + 5 = 9
\)
\(
9 + 7 = 16
\)
\(
16 + 9 = 25
\)
\(
25 + 11 = 36
\)
\(
36 + 13 = 49
\)
\(
49 + 15 = 64
\)
\(
64 + 17 = 81
\)
Thus, we have:
\(
P(X) = 81a
\)
Setting this equal to 1:
\(
81a = 1
\)
Solving for a:
\(
a = \frac{1}{81}
\)
Step 2: Calculate the probabilities
(i) Calculate \( P(X < 3) \)
To find \( P(X < 3) \), we need to sum the probabilities for \( X = 0, 1, 2 \):
\(
P(X < 3) = P(X=0) + P(X=1) + P(X=2)
\)
\(
= a + 3a + 5a = 9a
\)
Substituting the value of a:
\(
= 9 \times \frac{1}{81} = \frac{9}{81} = \frac{1}{9}
\)
(ii) Calculate \( P(X \geq 3) \)
To find \( P(X \geq 3) \):
\(
P(X \geq 3) = 1 - P(X < 3)
\)
\(
= 1 - \frac{1}{9} = \frac{8}{9}
\)
(iii) Calculate \( P(0 < X < 5) \)
To find \( P(0 < X < 5) \), we need to sum the probabilities for \( X = 1, 2, 3, 4 \):
\(
P(0 < X < 5) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
\)
\(
= 3a + 5a + 7a + 9a = 24a
\)
Substituting the value of a:
\(
= 24 \times \frac{1}{81} = \frac{24}{81} = \frac{8}{27}
\)
Final Answers
(i) The value of a is \( \frac{1}{81} \).
(ii) The probabilities are:
- \( P(X < 3) = \frac{1}{9} \)
- \( P(X \geq 3) = \frac{8}{9} \)
- \( P(0 < X < 5) = \frac{8}{27} \)
- P(X=0) = a
- P(X=1) = 3a
- P(X=2) = 5a
- P(X=3) = 7a
- P(X=4) = 9a
- P(X=5) = 11a
- P(X=6) = 13a
- P(X=7) = 15a
- P(X=8) = 17a
P(X) = a + 3a + 5a + 7a + 9a + 11a + 13a + 15a + 17a
\)
= a(1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17)
\)
1 + 3 = 4
\)
\(
4 + 5 = 9
\)
\(
9 + 7 = 16
\)
\(
16 + 9 = 25
\)
\(
25 + 11 = 36
\)
\(
36 + 13 = 49
\)
\(
49 + 15 = 64
\)
\(
64 + 17 = 81
\)
P(X) = 81a
\)
81a = 1
\)
a = \frac{1}{81}
\)
P(X < 3) = P(X=0) + P(X=1) + P(X=2)
\)
\(
= a + 3a + 5a = 9a
\)
= 9 \times \frac{1}{81} = \frac{9}{81} = \frac{1}{9}
\)
P(X \geq 3) = 1 - P(X < 3)
\)
\(
= 1 - \frac{1}{9} = \frac{8}{9}
\)
P(0 < X < 5) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
\)
\(
= 3a + 5a + 7a + 9a = 24a
\)
= 24 \times \frac{1}{81} = \frac{24}{81} = \frac{8}{27}
\)
- \( P(X < 3) = \frac{1}{9} \)
- \( P(X \geq 3) = \frac{8}{9} \)
- \( P(0 < X < 5) = \frac{8}{27} \)
Similar Questions
A random variable X has the follwing probability distribution:

Find P(0<X<4)
View SolutionIf random variable X has the following probability distribution. Then the value of a is

View SolutionIf a random variable X has the following probability distribution values of X
Then P(X≥6) is equal to

View SolutionA random variable X has the following probability distribution: Values of X: −2 −1 0 1 2 3 P(X):0.1 k 0.2 2k 0.3 k
View SolutionA random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution:
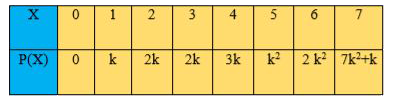
Determine : (i) k (ii) P(X<3) (iii) P(X>4)
View SolutionA random variable 'X' has the following probability distribution :

Find : (i) the value of K (ii) P(X≤1)
(iii) P(X≥0).
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionA random variable X has the following probability distribution:
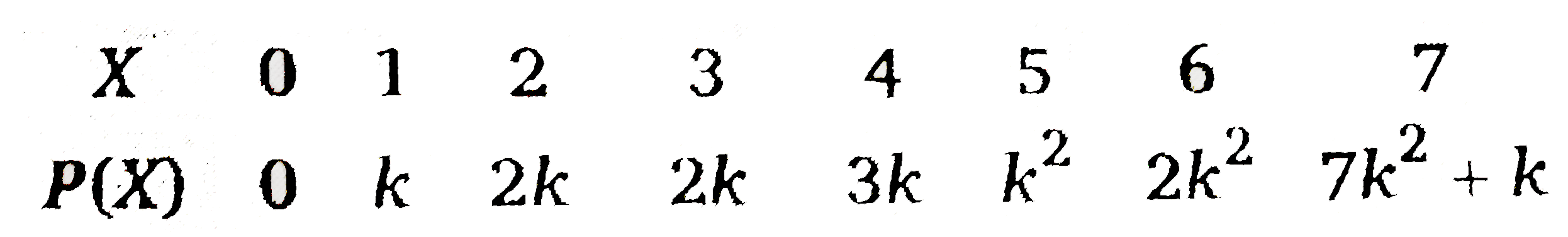
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution :

Determine
(i) k (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3).
View Solution
