A rubber ball is dropped from a height of 5m on a plane, where the acceleration due to gravity is not shown. On bouncing it rises to 1.8m. The ball loses its velocity on bouncing by a factor of
1625
25
35
925
To solve the problem of how much velocity the rubber ball loses upon bouncing, we can follow these steps:
Step 1: Calculate the velocity just before the ball hits the ground (V1)
When the ball is dropped from a height of 5 m, we can use the equation of motion:
V21=U2+2gh
Where:
- V1 = final velocity just before hitting the ground
- U = initial velocity (0 m/s, since it is dropped)
- g = acceleration due to gravity (we will keep it as g)
- h = height (5 m)
Substituting the values:
V21=0+2g⋅5
V21=10g
V1=√10g
Step 2: Calculate the velocity just after the ball bounces (V2)
After bouncing, the ball rises to a height of 1.8 m. We can use the same equation of motion to find the velocity just after the bounce:
V22=U2+2gh
Where:
- V2 = initial velocity just after the bounce
- U = final velocity at the peak (0 m/s, since it stops at the peak)
- h = height (1.8 m)
Substituting the values:
0=V22−2g⋅1.8
V22=2g⋅1.8
V22=3.6g
V2=√3.6g
Step 3: Calculate the loss of velocity
The loss of velocity due to bouncing can be calculated as:
Loss in velocity=V1−V2
Substituting the values we found:
Loss in velocity=√10g−√3.6g
Step 4: Calculate the factor by which the velocity is reduced
To find the factor by which the velocity is reduced, we can express it as a fraction of the initial velocity:
Factor of loss=V1−V2V1
Substituting the values:
Factor of loss=√10g−√3.6g√10g
This simplifies to:
Factor of loss=1−√3.6g√10g=1−√3.610=1−√0.36=1−0.6=0.4
Thus, the ball loses its velocity on bouncing by a factor of 25 or 0.4.
Final Answer:
The ball loses its velocity on bouncing by a factor of 25.
---
- V1 = final velocity just before hitting the ground
- U = initial velocity (0 m/s, since it is dropped)
- g = acceleration due to gravity (we will keep it as g)
- h = height (5 m)
V21=10g
V1=√10g
- V2 = initial velocity just after the bounce
- U = final velocity at the peak (0 m/s, since it stops at the peak)
- h = height (1.8 m)
V22=2g⋅1.8
V22=3.6g
V2=√3.6g
The ball loses its velocity on bouncing by a factor of 25.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A ball is dropped from a height of 10 m, as it falls,
Aits velocity increases and acceleration decreases.Bits velocity decreases and acceleration increases.Cits velocity increases and acceleration remains constant.Dits velocity and acceleration remains constant. - Question 2 - Select One
A ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
Ae2hBe√hCehD√eh - Question 3 - Select One
A ball is dropped from a height of 100 m. At the surface of the earth, 20% of its energy is lost. To what height the ball will rise?
A80mB20mC40mD60m
A ball is dropped from height 10 m . Ball is embedded in sand 1 m and stops, then
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
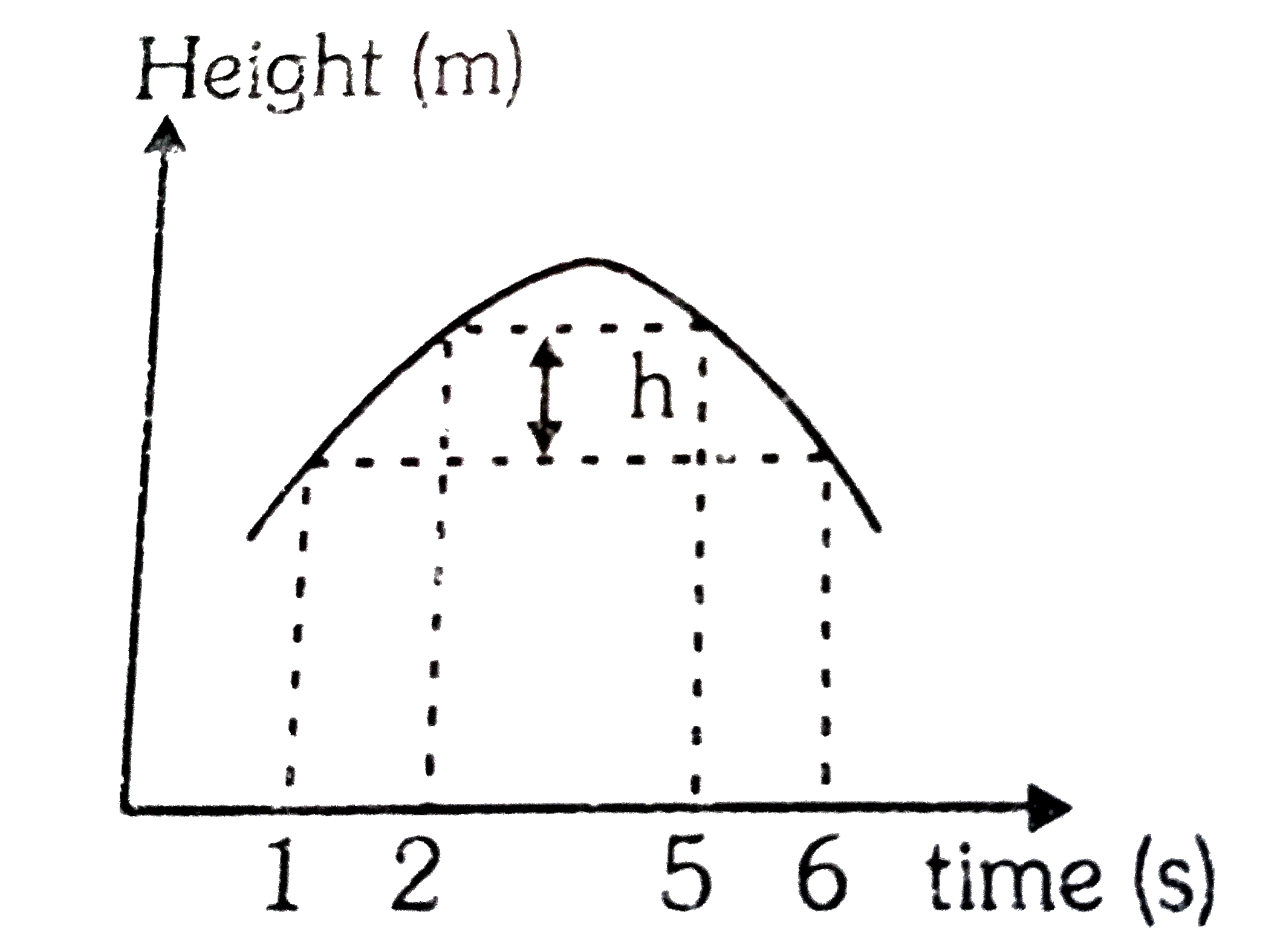 View Solution
View SolutionA ball is dropped onto a floor from a height of 10m. If 20% of its initial energy is lost,then the height of bounce is
View SolutionA ball is dropped from a height of 5 m, if it rebound upto height of 1.8 m, then the ratio of velocities of the ball after and before rebound is :
View SolutionA rubber ball dropped from 24 m height loses its kinetic energy by 25%. What is the height to which it rebounds?
View Solution

