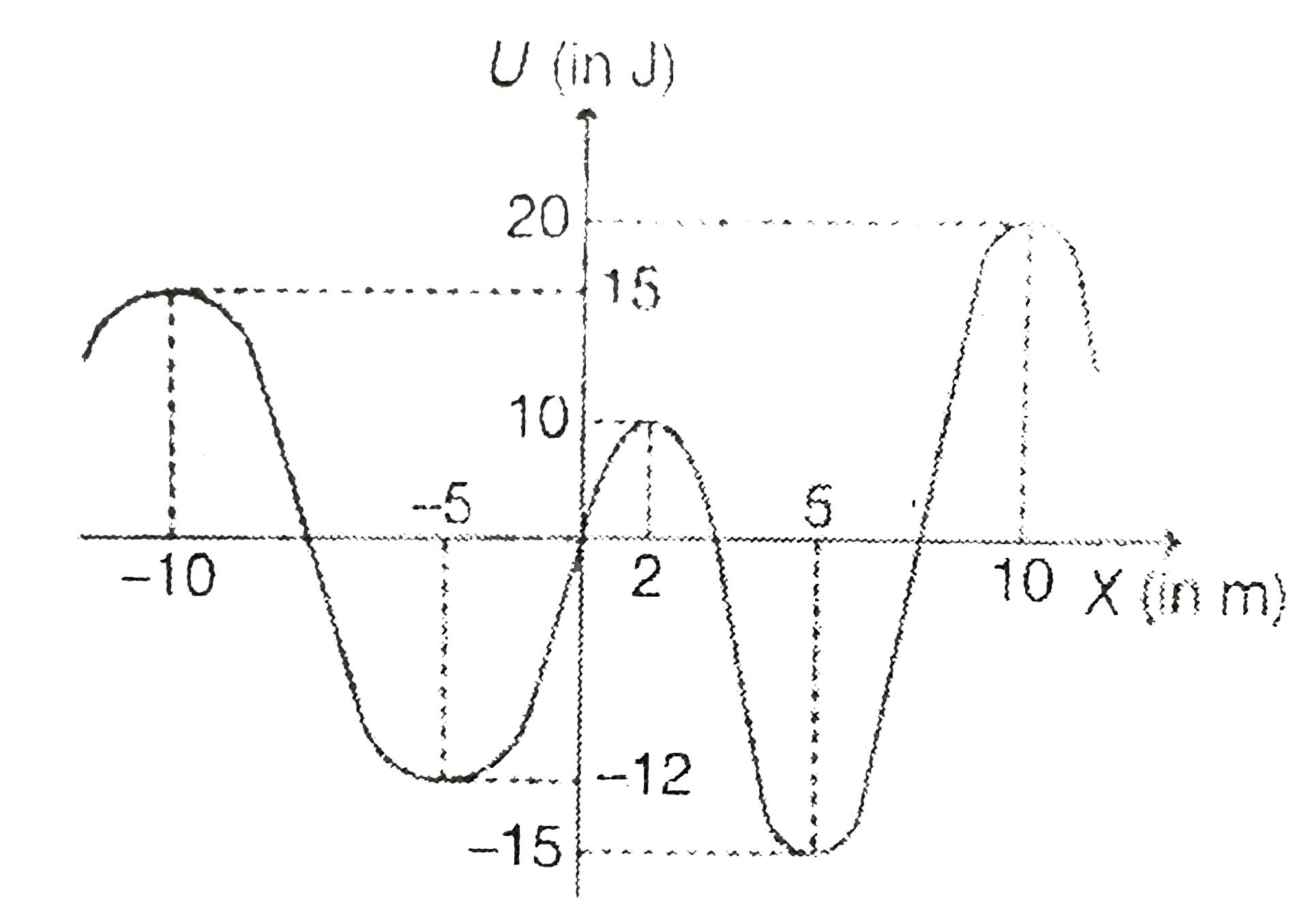
In the figure the variation of potential energy of a particle of mass is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
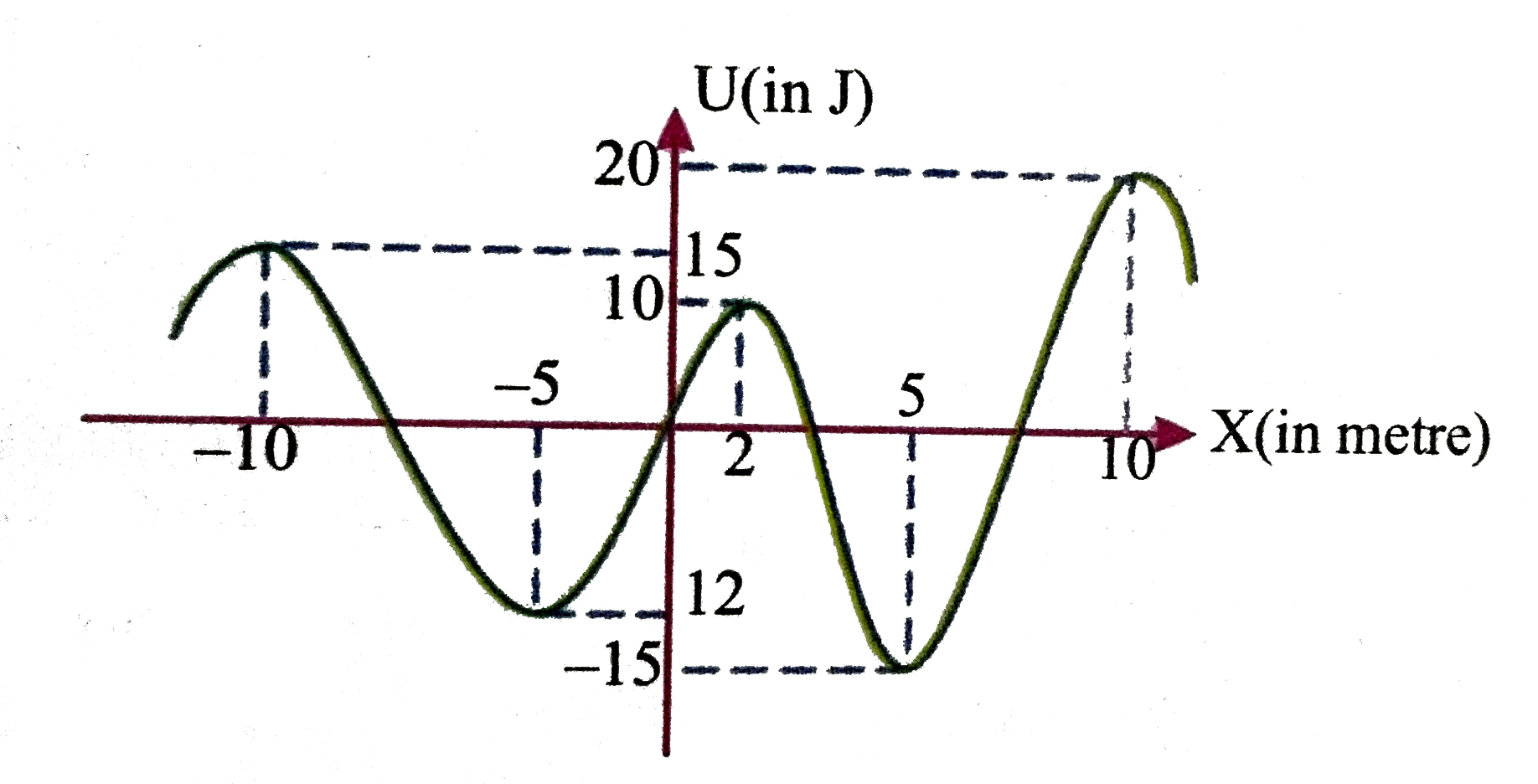
If the particle is released at the origin then
it will move towards positive x-axis
it will move towards negative x-axis
it will remain stationary at the origin
its subsequent motion cannot be decided due to lack of information
Step by step video & image solution for In the figure the variation of potential energy of a particle of mass m = 2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis. If the particle is released at the origin then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
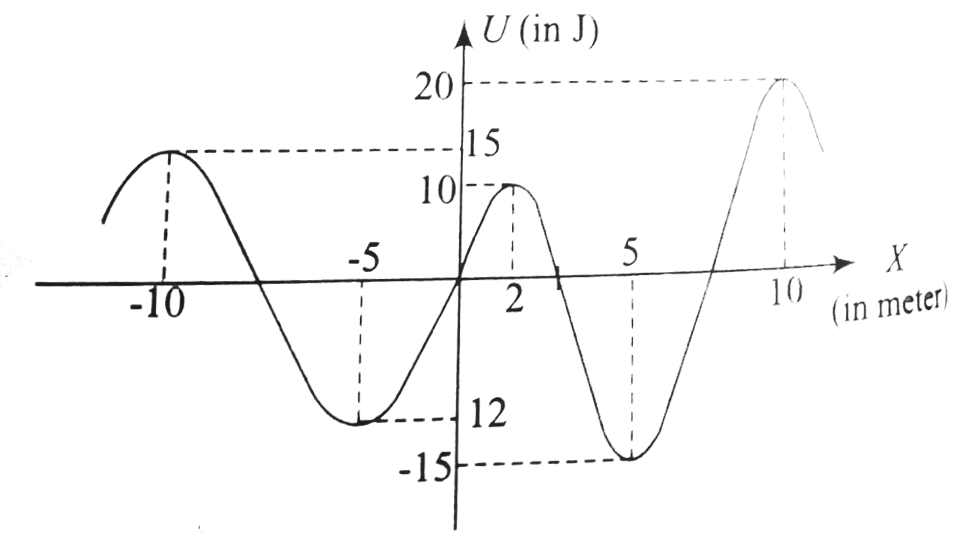
In the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis. Which of the following statements are correct about the particle:View SolutionIn figure, the variation of potential energy of a particle of mass m=2kg is represented w.r.t its x-coordinate. The particle moves under the effect of the conservative force along the x-axis. Which of the following statements is incorrect about the particle?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
If the particle is released at the origin, thenAit will move towards positive x-axisBit will move towards negative x-axisCit will remain stationary at the originDEither of (a) or (b) - Question 2 - Select One
In the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
If the particle is released at x=2+Δ where Δ→0 (it is positive), then its maximum speed in subsequent motion will beA√10m/sB5m/sC5√2m/sD7.5m/s - Question 3 - Select One
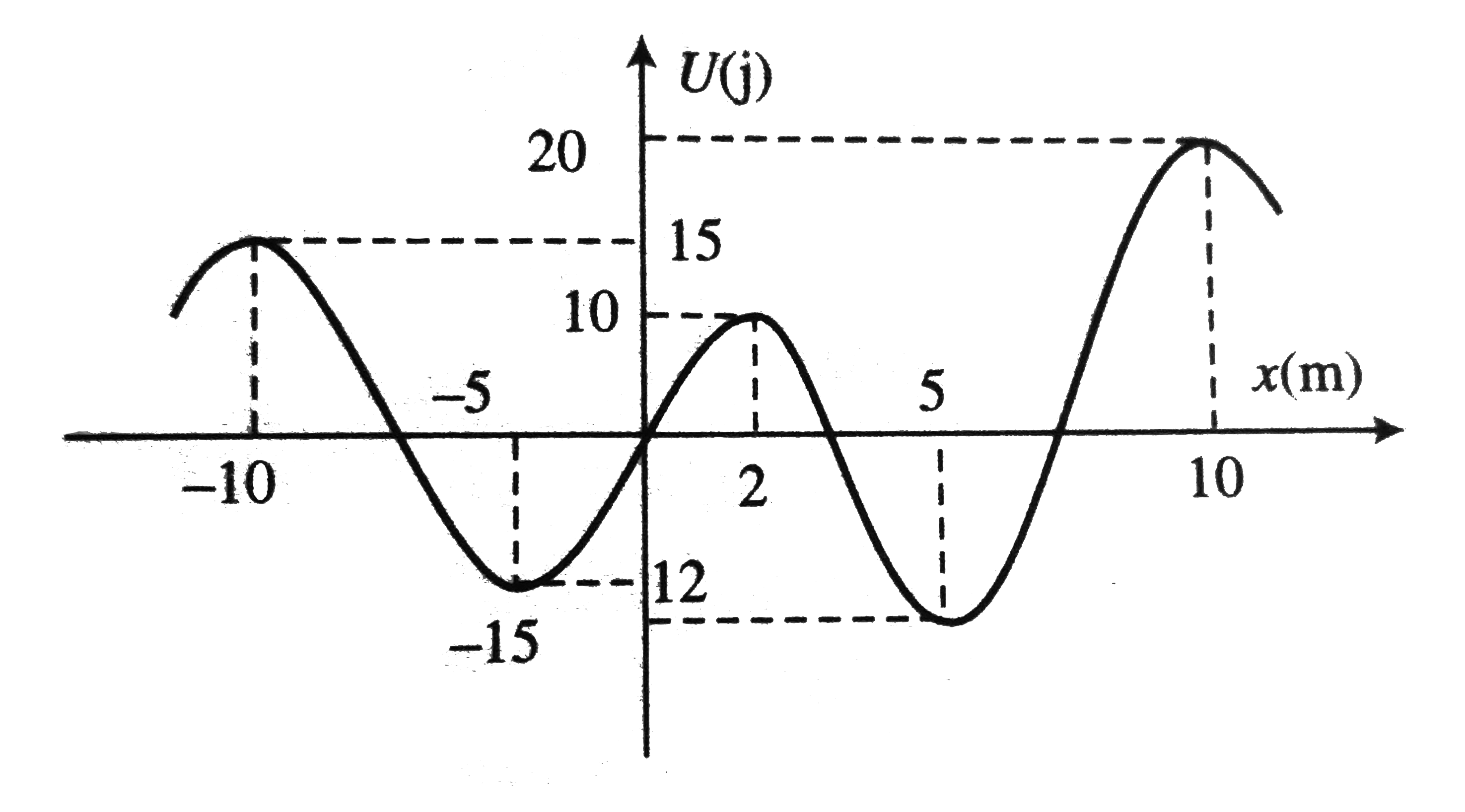
In the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
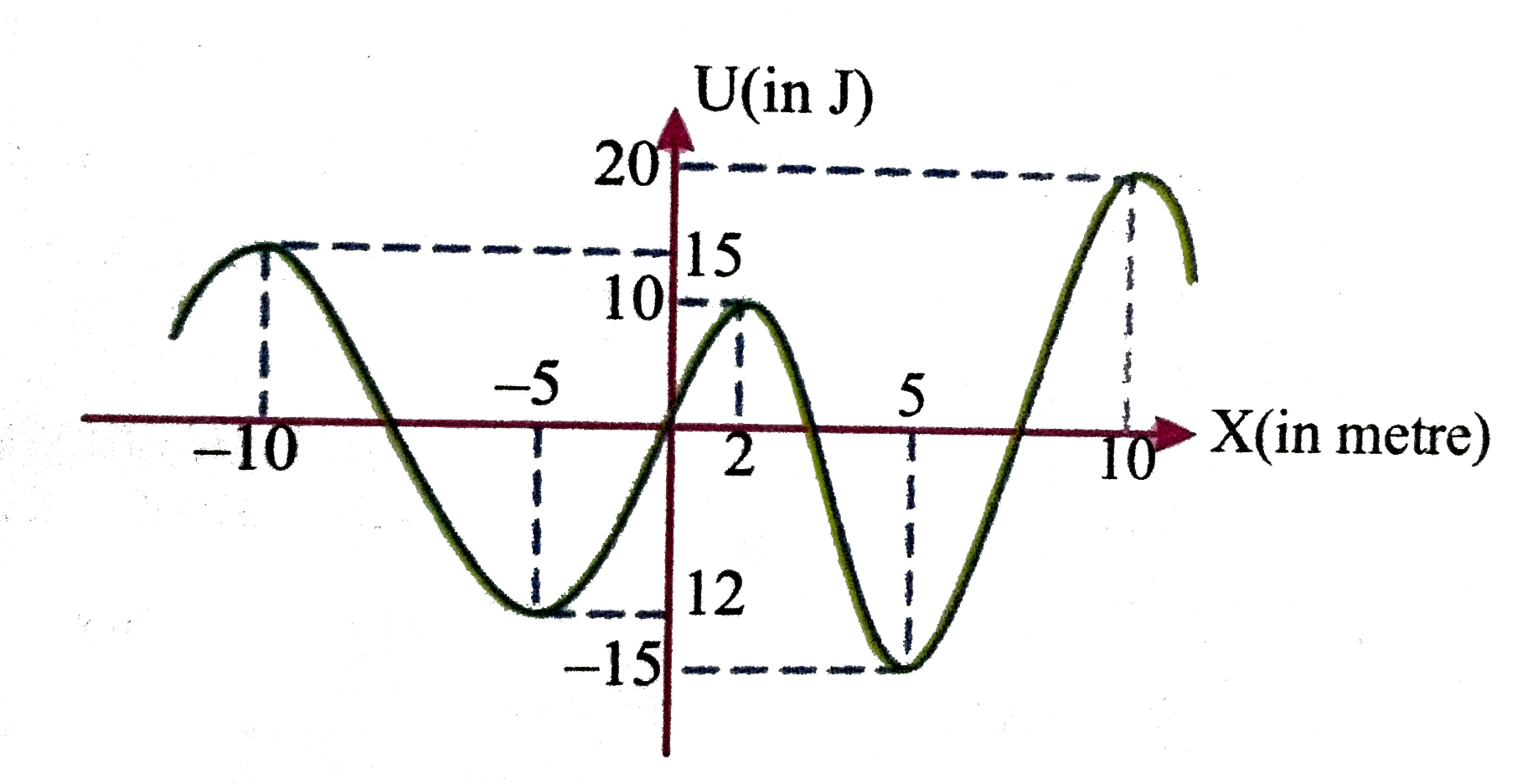
x=−5m and x=10m position of the particle are respectively ofAneutral and stable equilibrium.Bneutral and unstable equilibrium.Cunstable and stable equilibrium.Dstable and unstable equilibrium.
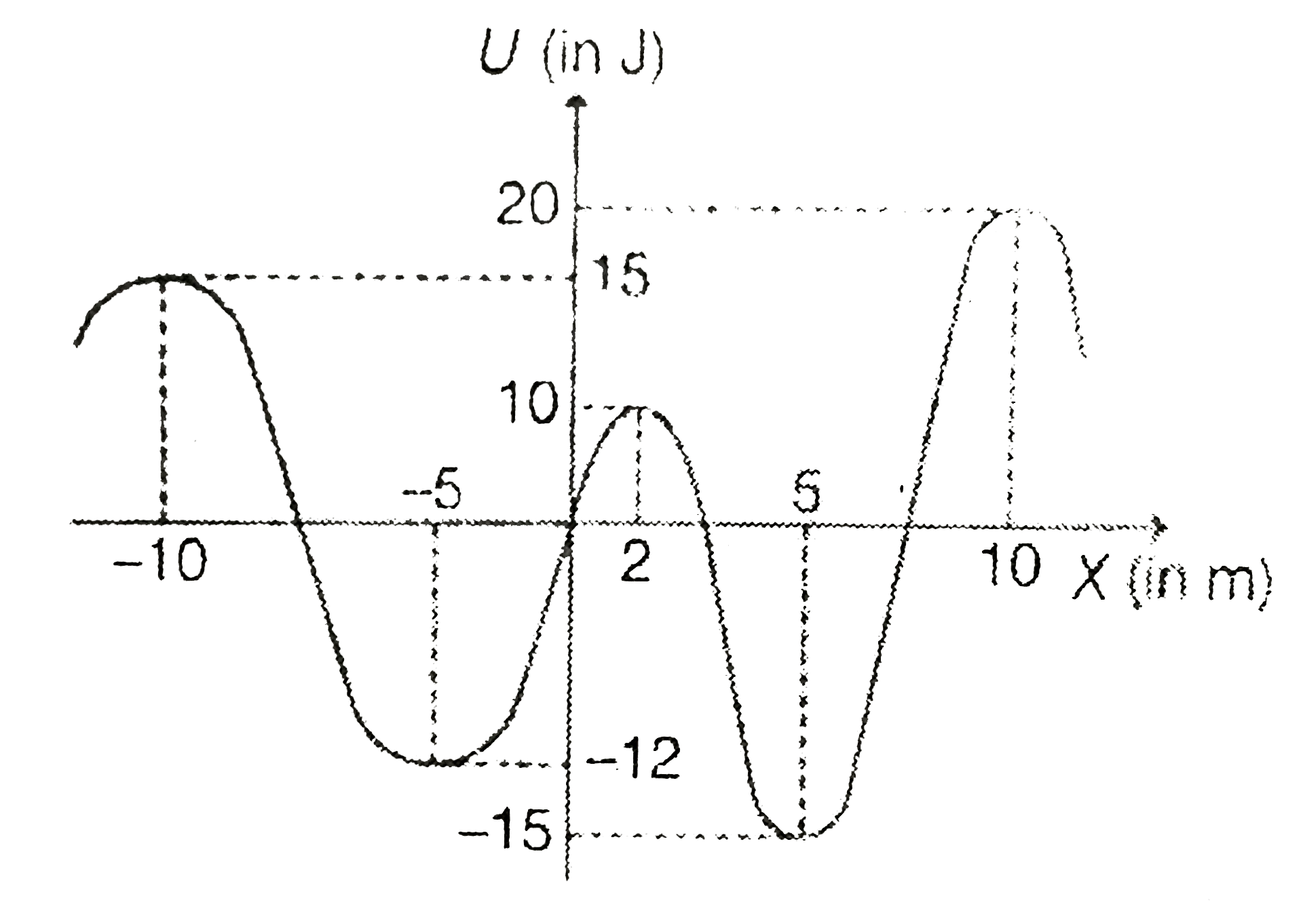
The variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
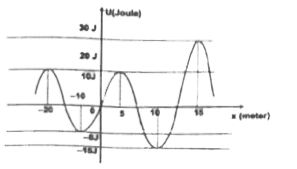 View Solution
View SolutionThe potential energy of a particle moving along x-axis is given by U=20+5sin(4πx), where U is in J and x is in metre under the action of conservative force :
View SolutionIn the figure the variations of componets of acceleration of particles of mass 1kg is shown w.r.t. time. The initial velocity of the particle is →u=(−3ˆi+4ˆj)m/s. the total work done by the resultant force on the particles in time intervals from t=0 to t=4 seconds is :
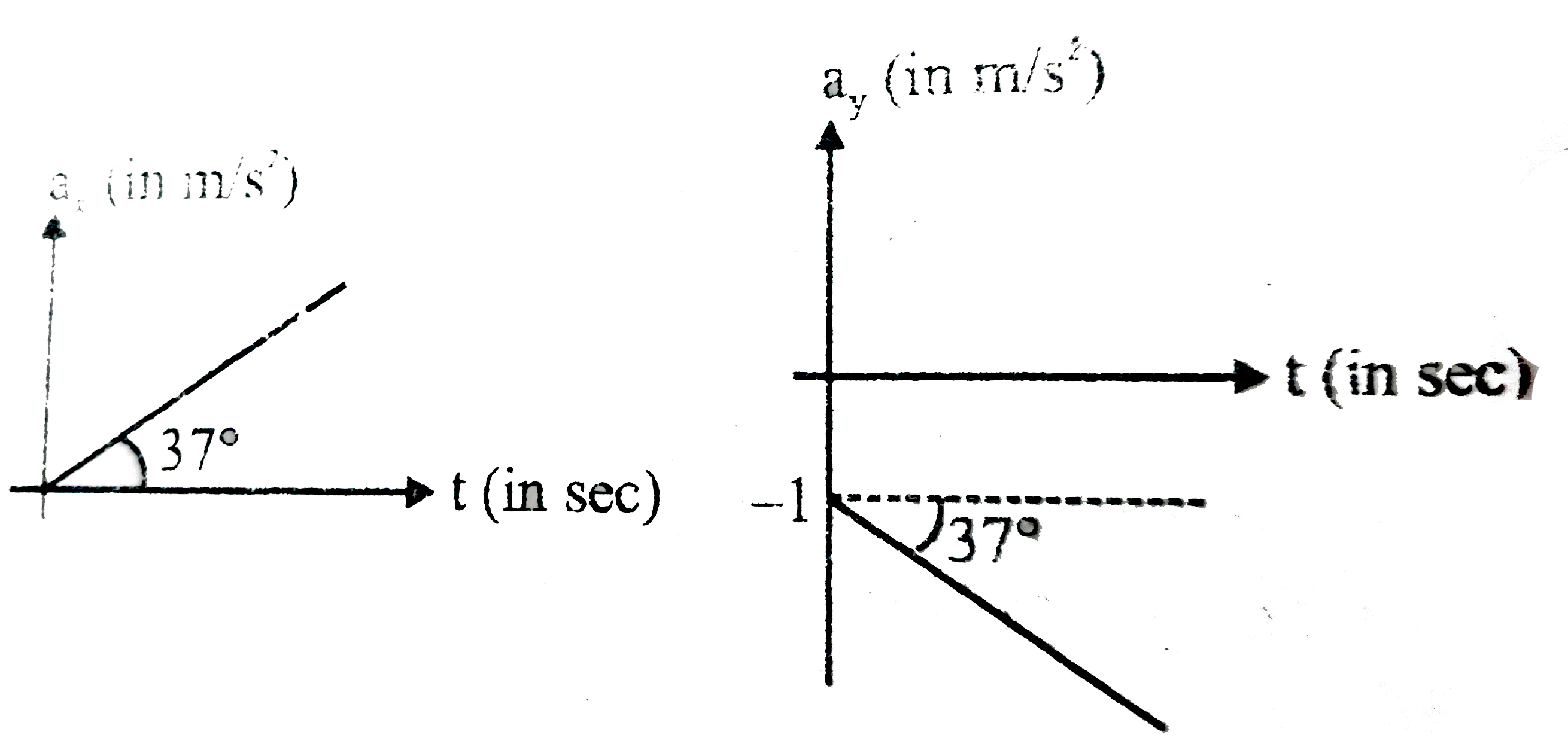 View Solution
View SolutionForce acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
Now consider another situation. A force →F=(4ˆi+3ˆj)N acts on a particle of mass 2kg. The particle under the action of this force moves from the origin to a point A (4m,−8m). Initial speed of the particle, i.e., its speed at the origin is 2√6ms−1. Figure shows three paths for the motion of the particle from O to A.
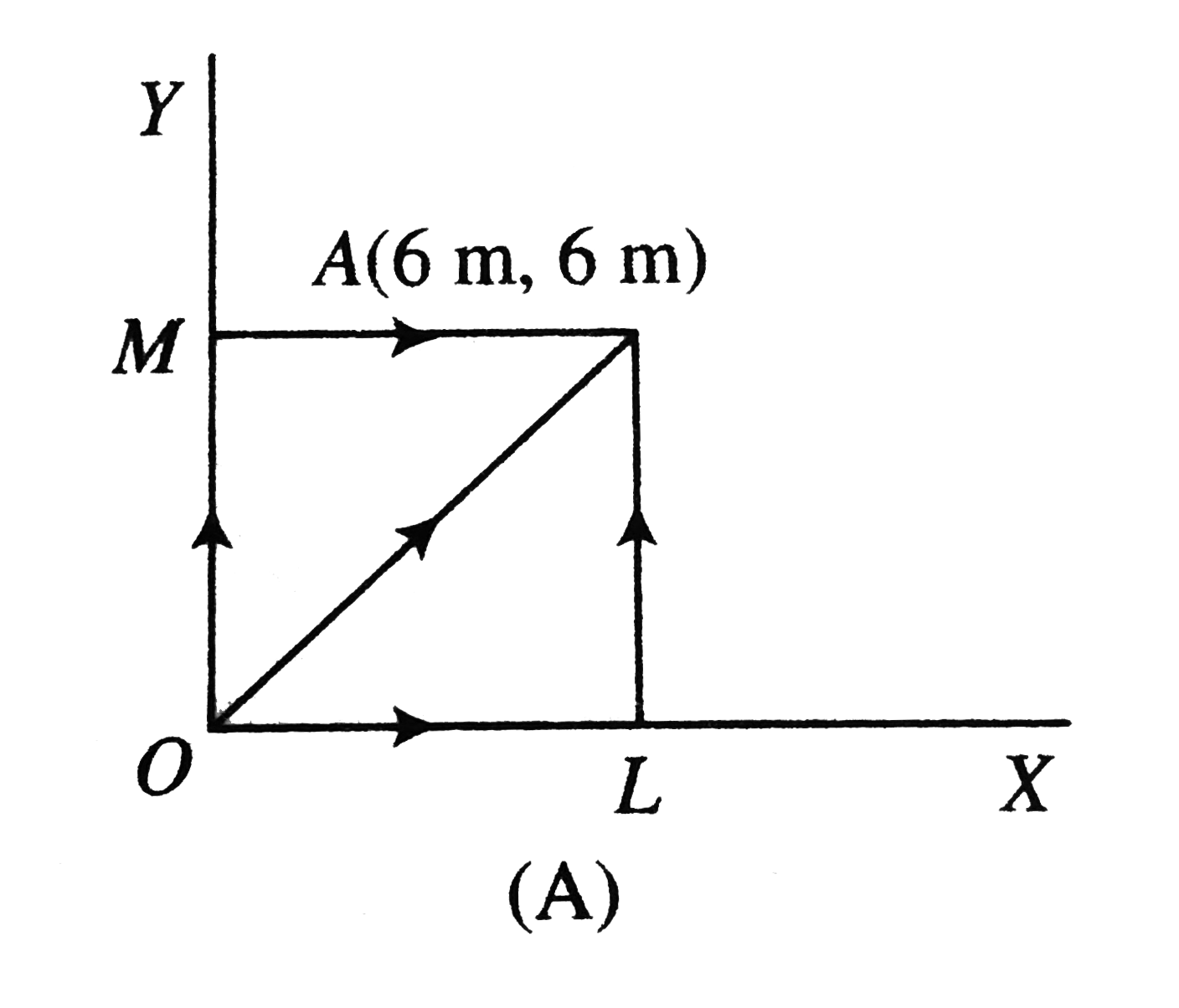
If the potential energy at O is 16J, the potential energy at A will beView SolutionThe potential energy of a particle of mass 2 kg moving in a plane is given by U=(−6x−8y)J. The position coordinates x and y are measured in meter. If the particle is initially at rest at position (6, 4)m, then
View Solution

