Two concentric, thin metallic spheres of radii R1 and R2 (R1>R2) bear charges Q1 and Q2 respectively. Then the potential at distance r between R1 and R_(2) will be
K(Q1+Q2r)
K(Q1r+Q1R2)
K(Q2r+Q1R1)
K(Q1R1+Q2R2)
To find the potential at a distance r between two concentric metallic spheres of radii R1 and R2 (where R1>R2), bearing charges Q1 and Q2 respectively, we can follow these steps:
Step 1: Understand the Configuration
We have two concentric metallic spheres:
- The outer sphere has radius R1 and charge Q1.
- The inner sphere has radius R2 and charge Q2.
Step 2: Determine the Charge Distribution
Using Gauss's Law, we know that:
- The electric field inside a conductor in electrostatic equilibrium is zero.
- Therefore, the inner surface of the outer sphere will have a charge of −Q2 to balance the charge of the inner sphere.
- The outer surface of the outer sphere will then have a charge of Q1+Q2.
Step 3: Calculate the Potential at Distance r
For a point at distance r between R1 and R2 (i.e., R2<r<R1):
1. The potential V(r) due to the inner sphere (charge Q2) at distance r is given by:
Vinner=kQ2r
where k is Coulomb's constant.
2. The potential due to the outer sphere (charge Q1+Q2) is constant throughout the space outside the inner sphere and is given by:
Vouter=kQ1+Q2R1
Step 4: Combine the Potentials
The total potential V(r) at distance r is the sum of the potentials due to both spheres:
V(r)=Vinner+Vouter
Substituting the expressions we derived:
V(r)=kQ2r+kQ1+Q2R1
Step 5: Final Expression
Thus, the potential at distance r between the two spheres is:
V(r)=kQ2r+kQ1+Q2R1
We have two concentric metallic spheres:
- The outer sphere has radius R1 and charge Q1.
- The inner sphere has radius R2 and charge Q2.
Using Gauss's Law, we know that:
- The electric field inside a conductor in electrostatic equilibrium is zero.
- Therefore, the inner surface of the outer sphere will have a charge of −Q2 to balance the charge of the inner sphere.
- The outer surface of the outer sphere will then have a charge of Q1+Q2.
For a point at distance r between R1 and R2 (i.e., R2<r<R1):
1. The potential V(r) due to the inner sphere (charge Q2) at distance r is given by:
Vinner=kQ2r
where k is Coulomb's constant.
Vouter=kQ1+Q2R1
The total potential V(r) at distance r is the sum of the potentials due to both spheres:
V(r)=Vinner+Vouter
Substituting the expressions we derived:
V(r)=kQ2r+kQ1+Q2R1
Thus, the potential at distance r between the two spheres is:
V(r)=kQ2r+kQ1+Q2R1
Topper's Solved these Questions
Similar Questions
Two concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out total energy of the system.
 View Solution
View SolutionTwo concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out potential
(i) at point (ii) at surface of smaller shell (i.e. at point B)
(iii) at surface of larger shell (i.e. at point C) (iv) at r≤R1
(v) at R1≤r≤R2 (vi) at r≥R2View Solution
Knowledge Check
- Question 1 - Select One
The concentric, thin metallic spheres of radii r1 and r2(r1>r2) carry charges q1 and q2 respectively. Then the electric potential at distance r(r2<r<r1) will be 14πε0 times
Aq1+q2rBq1r1+q2rCq1r2+q2r2Dq1r2+q2r1 - Question 2 - Select One
The insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
ANo change in the electrical energy of the systemBAn increase in the electrical energy of the systemCAlways a decrease in the electrical energy of the systemDA decrease in electrical energy of the system until Q1R2=Q2R3 - Question 3 - Select One
The capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
A4πε0R2B4πε0(R2−R1)R1R2C4πε0R1R2(R2−R1)D4πε0R1
You are given two concentric charged conducting spheres of radii R1andR2 such that R1>R2, having charges Q1andQ2 respectively and uniformly distributed over its surface. Calculate E and V at three points A, B , C whose distances from the centre are rA,rBandrc respectively as shown in figure.
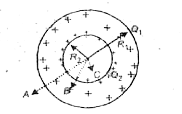 View Solution
View SolutionTwo concentric uniformly charge spherical shells of radius R1 and R2(R2>R1) have total charges Q1 and Q2 respectively. Derive an expression of electric field as a function of r for following positions.
(i) r<R1 (ii) R1≤r<R2
(iii) r≥R2
 View Solution
View SolutionTwo non-conduction hollow uniformly charged spheres of radil R1 and R2 with charge Q1 and Q2 respectively are places at a distance r. Find out total energy of the system.
 View Solution
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionTwo conducting spheres of radii r1 and r2 having charges Q1 and Q2 respectively are connected to each other. There is
View Solution

