You are given two concentric charged conducting spheres of radii $R_{1} and R_{2}$ such that $R_{1} > R_{2},$ having charges $Q_{1} and Q_{2}$ respectively and uniformly distributed over its surface. Calculate E and V at three points A, B , C whose distances from the centre are $r_{A}, r_{B} and r_{c}$ respectively as shown in figure.

Text Solution

Verified by Experts

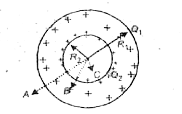
At point A , the point A is outside both the spheres so for the purpose of calculation of E and V we have to consider both $Q_{1} and Q_{2}$ to be concentrated at the centre.
So, E $\frac{(Q_{1} + Q_{2})}{4 π ε_{0} . r_{A}^{2}} and V = \frac{(Q_{1} + Q_{2})}{4 π ε_{0} . r_{A}}$
At point B : For electric field calculation note that the point B is inside the outer sphere so there will be no contribution of $Q_{1}$ in the electric field at B. But for $Q_{2}$ charges, the point B is outside so we have t assume $Q_{2}$ to be at the centre and distance of B will be taken to be $r_{B}$
So, $e a t B = \frac{Q_{2}}{4 π ε_{0} r_{B}^{2}}$
Now, for potential, remember that a single charge will never give zero contribution to potential at finite pionts.
So $Q_{1}$ as well as $Q_{2}$ will contribute to potential at B. Noe talk about the contribution of $Q_{1}$ at point B you can see that the point B is inside the large sphere of $Q_{1}$ so $Q_{1}$ will offer its surface potential $\frac{Q_{1}}{4 π ε_{0} R_{1}}$ at all its inside points. but what about the potential contribution of $Q_{2}$ at point B! for $Q_{2}$ the point B is outside the sphere so, we'll assume as if $Q_{2}$ is concentrated at the centre and the distance taken will be $r_{B}$ . so the contribution of $Q_{2}$ in potential will be $\frac{Q_{2}}{4 π ε_{0} r_{B}}$
Hence the total potential at B = $\frac{Q_{1}}{4 π ε_{0} R_{1}} + \frac{Q_{2}}{4 π ε_{0} r_{B}}$
At point C :
For electric field note that to both $Q_{1} and Q_{2}$ . the point c is inside. So, the net contribution in the electric field will be zero, i.e E at C = zero. infact, at all the point inside the smaller sphere, the electric field will be zero,
whate about potential at C! For both the spheres the point C is inside so both $Q_{1} and Q_{2}$ will offer
their respective surface potential. since surface potential of $Q_{1}$ is $\frac{Q_{1}}{4 π ε_{0} R_{1}}$ and that of $Q_{2}$ is $\frac{Q_{2}}{4 π ε_{0} R_{2}}$ , hence the potential at C will be $\frac{Q_{1}}{4 π ε_{0} R_{1}} + \frac{Q_{2}}{4 π ε_{0} R_{2}}$
In fact at all the points inside the inner sphere the potential will be constant and will be equal to the potential at C.

Updated on:21/07/2023