In the arrangement shown in the fig the cylinder is insulating one. Both sides same diatomic gas is trapped by two insulting massless pistos with the help of an ideal spring. The natural length of the spring is equal to the length of the cylinder. initial state of the gases are as shown in the figure.

What is the value of energy stored in the spring ?
P0V0
2P0V0
4P0V0
P0V02
The correct Answer is:A
If x be the initial length of the gas chambers & A be the area of cross section of the cylinder then,
x=V0A Also P0A=2kx
P0x=2kξmpliesP0V0=2kx2
∴12k(2x)2=12k4x2=2kx2=P0V0
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A thermally insulated vessel is divided in to two parts by a heat insulating piston which can move in the vessel without the friction. The left part of the vessel contains one mole of an ideal monatomic gas, & the right part is empty. The piston is connected to the right wall of the vessel through a spring whose length in free state is equal to the length of the vessel as shown in the figure. Determine the heat capacity C of the system, neglecting the heat capacity of the vessel, piston and spring.

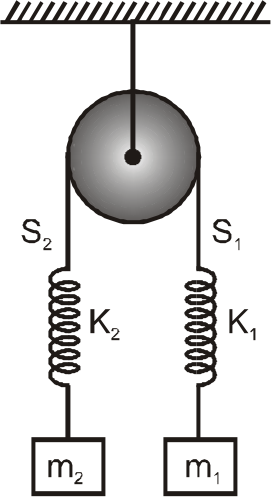
View SolutionConsider the condition shown in the figure. Pulley is massless and frictionless, springs are massless. Both the blocks are released with the springs in their natural lengths. Choose the correct options.
View Solution
Knowledge Check
In the arrangement shown in the fig the cylinder is insulating one. Both sides same diatomic gas is trapped by two insulting massless pistos with the help of an ideal spring. The natural length of the spring is equal to the length of the cylinder. initial state of the gases are as shown in the figure.

Now the gases are heated slowly, such that their temperature becomes three times to their initial temperature. The total heat given to the system isA12P0V0B8P0V0C5P0V0D6P0V0Each of the above three springs are identical (they have the same equilibrium length and spring constant k). They are fixed together as shown in figure. What is the effective spring constant of the assembly?
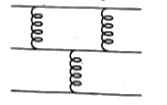 AkB(23)kC(12)kD(13)k
AkB(23)kC(12)kD(13)kConsider the condition shown in the figure. Pulley is massless and frictionless, springs are massless. Both the blocks are released with the springs in their natural lengths. Choose the correct options.
 AMaximum elongation in the spring S1 is 4m1m2gK1(m1+m2)BMaximum elongation in the spring S1 is 4m1m2gK2(m1+m2)CIf m1=m2 both the blocks will come to instantaneous rest simultaneously.DIf K1=K2 both the blocks will come to instantaneous rest simultaneously.
AMaximum elongation in the spring S1 is 4m1m2gK1(m1+m2)BMaximum elongation in the spring S1 is 4m1m2gK2(m1+m2)CIf m1=m2 both the blocks will come to instantaneous rest simultaneously.DIf K1=K2 both the blocks will come to instantaneous rest simultaneously.
Consider a gas filled in a part of thermally insulated vessel with frictionless insulated piston (connected to a massless spring). Natural length of the spring equals length of the vessel. For 30 J of heat supplied, internal energy of gas increases by 25 J. find the number of atoms in one molecule.
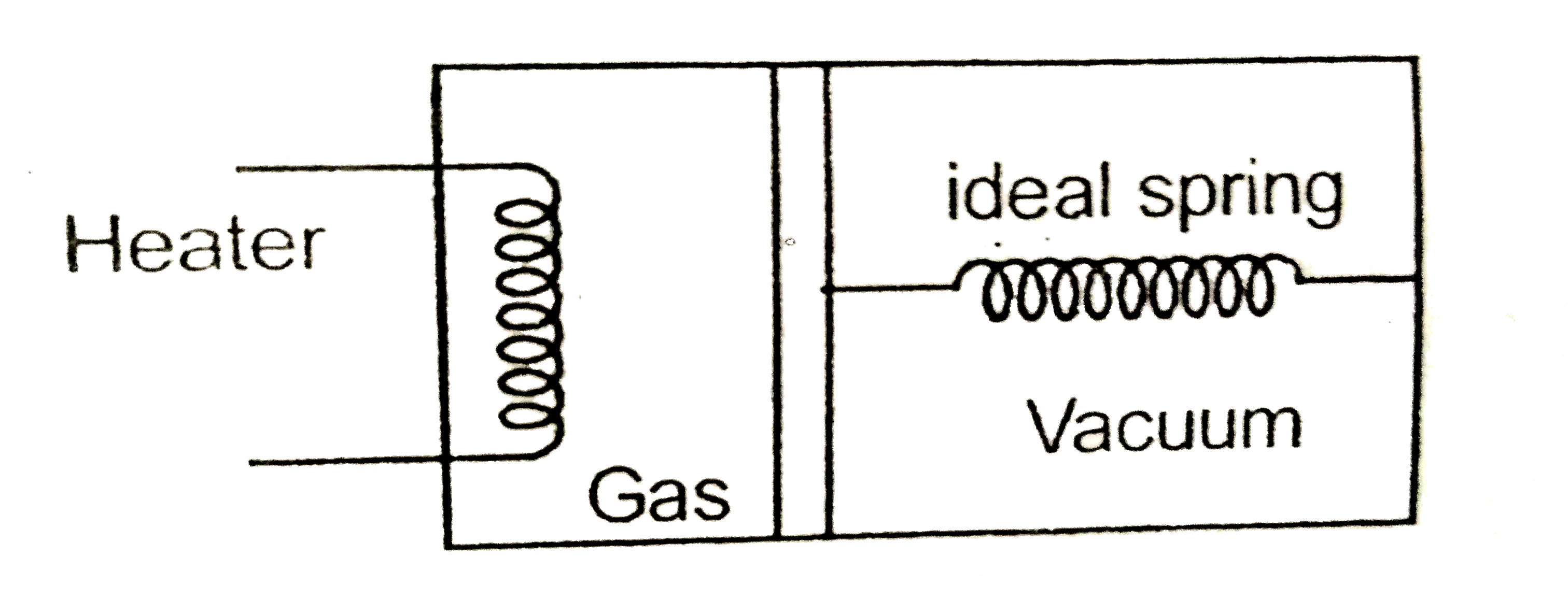
View SolutionConsider a gas filled in a part of thermally insulated vessel with frictionless insulated piston (connected to a massless spring). Natural length of the spring equals length of the vessel. For 30 J of heat supplied, internal energy of gas increases by 25 J. find the number of atoms in one molecule.

View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When the spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length

View SolutionA dumbbell consists of two balls A and B of mass m=1 kg and connected by a spring. The whole system is placed on a smooth horizontal surface as shown in the figure. Initially the spring is at its natural length, the ball B is imparted a velocity v0=8√7m/s in the direction shown. The spring constant of the spring is adjusted so that the length of the spring at maximum elongation is twice that of the natural, length of the spring. Find the maximum potential energy stored (in Joule) in the spring during the motion.

View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When thye spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length

View Solution
