There is a hollow cylinder of radius R and it is rotating with constant angular speed ω. There is a point mass which rotates along with the cylinder and geta carried upward. Friction is enough such that the point mass does not slip with respect to the cylinder as long as the normal force is becomes zero. If the path of the particle after it lost contact with the cylinder is as shown in the figure then,

What is the value of ω (in terms of g and R)
√g√3R
√g2√πR
√g2R
√g√2R
The correct Answer is:D
12gsinθ.4v2g2cos2θ=2R……..(1)

v2=Rgsinθ……(2)
From (1) and (2) tanθ=1
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
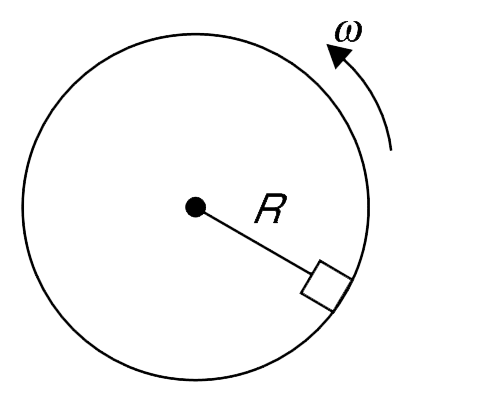
A cylinder with radius R spins about its horizontal axis with angular speed ω. There is a small block lying on the inner surface of the cylinder. The coefficient of friction between the block and the cylinder is μ. Find the value of ω for which the block does not slip, i.e., stays at rest with respect to the cylinder.
View SolutionAn infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View Solution
Knowledge Check
There is a hollow cylinder of radius R and it is rotating with constant angular speed ω. There is a point mass which rotates along with the cylinder and geta carried upward. Friction is enough such that the point mass does not slip with respect to the cylinder as long as the normal force is becomes zero. If the path of the particle after it lost contact with the cylinder is as shown in the figure then,

In Order to happen this where most the particle lose contact with the cylinder?Ah=R2Bh=R√3Ch=R√2Dh=R√πA solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
In a gravity free space, a hollow cylinder of radius 4R and mass M is being rotated by a constant angular velocity ω clockwise w.r.t. an inertial frame of reference. Another hollow cylinder of radius R and mass m is rotating inside this cylinder, such that it touches the inner surface of larger cylinder without slipping and its centre of mass appears stationery from inertial frame Dynamic friction coefficient between cylinders is μ. If the normal reaction between cylinders is denoted by N, answer the following questions.
What is the angular velocity of smaller cylinder.

View SolutionA solid cylinder of mass 'M' and radius 'R' is rotating along its axis with angular velocity ω without friction. A particle of mass 'm' moving with velocity v collides aganist the cylinder and sticks to its rim. After the impact calculate angular velocity of cylinder .
View SolutionIn a gravity free space, a hollow cylinder of radius 4R and mass M is being rotated by a constant angular velocity ω clockwise w.r.t. an inertial frame of reference. Another hollow cylinder of radius R and mass m is rotating inside this cylinder, such that it touches the inner surface of larger cylinder without slipping and its centre of mass appears stationery from inertial frame Dynamic friction coefficient between cylinders is μ. If the normal reaction between cylinders is denoted by N, answer the following questions.
What is the value of N

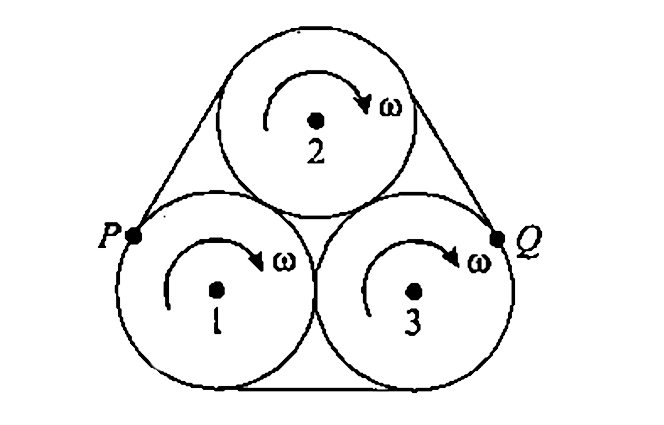
View SolutionThree identical cylinders of radius R are in contact.Each cylinder is rotating with angular velocity ω.A thin belt is moving without sliding on the cylinders. Calculate the magnitude of velocity of point P with respect to Q.P and Q are two points of belt which are in contact with the cylinder.
View SolutionA hollow cylinder of radius R rotates about its axis which is vertical. A block remains in contact with the inner wall if the frequency of rotation is f hertz, but falls at lower frequaencies. The coefficient of friction between the block and the cylinder is
View Solution
