A positively charged particle is given an initial velocity v0 in XY plane as shown in diagram. Initially the particle was at origin and the region contains uniform, mutually perpendicular electric and magnetic field. Let →E=−Eˆj and →B=Bˆk. The minimum magnitude of the magnetic field so that the charge particle crosses the origin again during its subsequenty motion is Bmin=nπEv0, find the integer value n

The correct Answer is:2
→v=v02(√3ˆi+ˆj)
For corssing orign,
k2πmqB=2(v0/2)qE/m,k is an integer
⇒B=(2πEv0)k
For minimum value, k=1
⇒Bmin=2πEv0
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A charge particle enters into a region containing uniform electric field (E) and uniform magnetic field (B) along x-axis and y-axis respectively.If it passes the region undeviated the velocity of charge particle is given by
View SolutionA charge particle enters into a region containing uniform electric field (E) and uniform magnetic field (B) along x- axis and y-axis respectively.If it passes the region undeviated the velocity of charge particle is given by
View Solution
Knowledge Check
A charged particle enters a magnetic field B with its initial velocity v making an angle of π4 and B. The path of the particle will be
Aa straight lineBa circleCan ellipseDa helixA charged particle goes undeflected in a region containing uniform electric and magnetic field.It is not possible at all (→υ=velocity of particle,→E=uniform electric field,→B=uniform magnetic field)
A→E∣∣∣∣→B,→υ∣∣∣∣→EB→E is not collinear to →BC→υ∣∣→Bbut →E is not collinear to →BD→E∣∣→Bbut →υ is not collinear to →EA n electrically charged particle enters into a uniform magnetic induction field in a direction perpendicular to the field with a velocity v then it travels
Aina straight line without accelerationBwith force in the direction of the fieldCin a circular path with a radius directly proportional toDin a circular path with a radius directly proportional to its velocity
A particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by
→B=−B0→Jand→E=E0→K.
Find the speed of the particle as a function of its z-coordinate.
View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by
→B=−B0→Jand→E−E0→K.
Find the speed of the particle as a function of its z-coordinate.
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find

distance travelled in the magnetic field
View SolutionA positive charge particle to charge q& mass m is released at origin.There are unifrom magnetic and electric field in the space given by →E=E0ˆj&→B=B0ˆk, where E0&B0 are constants.Find the y coordinate of the particle at time t.
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
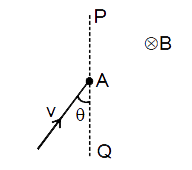
impulse of magnetic force.
View Solution
