Two capacitors
C1=C2=1π2×10−2F and inductor L=2×10−2H are connected in series as shown in the figure. Initially charge on each capacitors are 4√3μC. At t=0 switch S1 is closed at t=1/400 sec, switch S2 is also closed. The maximum charge on capacitor C2 during LC oscillation is k√3μC. Find k

The correct Answer is:6
ω=1√LCeq=100π
⇒T=1/50 sec
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
In circuit shown in figure charge on capacitor is Q=100μC. If switch is closed at t=0 find current in circuit when charge on capacitor reduces to 50μC. Also find the maximum current in circuit.

View SolutionIn the circuit shown, the capacitor initially charged with a 12V batteryy, when switch S1 is open and switch S2 is closed. The maximum value of current in the circuit when S2 is opened and S2 is closed is

View Solution
Knowledge Check
In the circuit shown, the capacitor initially charged with a 12V batteryy, when switch S1 is open and switch S2 is closed. The maximum value of current in the circuit when S2 is opened and S2 is closed is
 A10−6AB7.2μAC720μAD360μA
A10−6AB7.2μAC720μAD360μAThree capacitors (of capacitances C, 2C and 3C) and three resistors (of resistance R, 2R and 3R) are connected with a battery and switch S as shown in the figure. When switch S is open, charges on the capacitors are shown. Switch S is closed at t=0sec. The time constant of the circuit will be
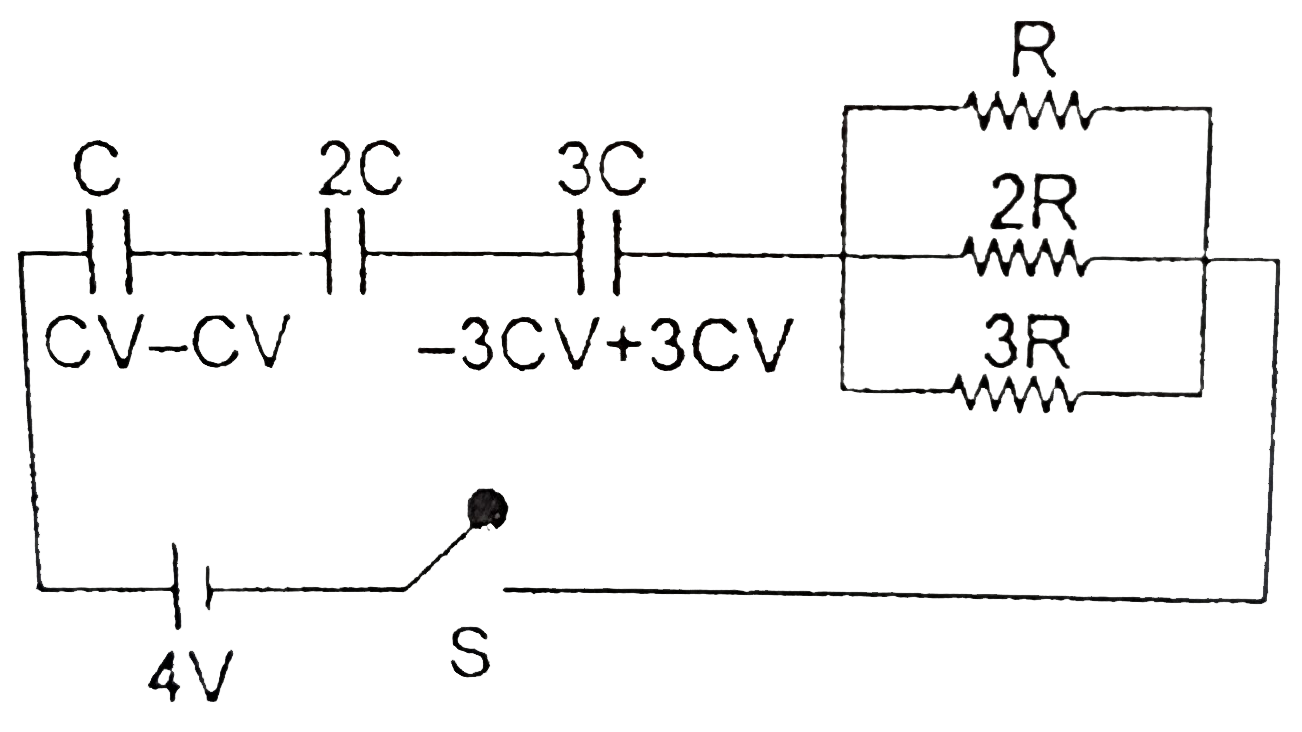 ARCB6RC11C36RC121DNone
ARCB6RC11C36RC121DNoneTwo capacitor C1 and C2, charged with chargesq1 and q2 then these are connected in series with an uncharged capacitor C, as shown in figure. As the switch S is closed :
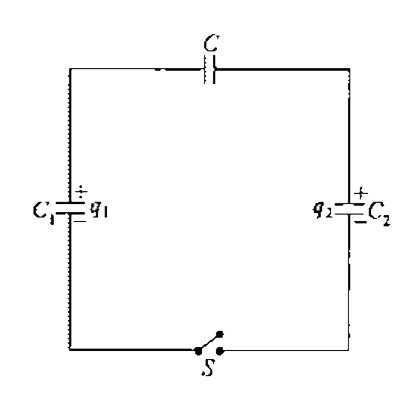 AC gets charged in any conditionBC gets charged only when q1C2>q2C1CC gets charged only when q1C2<q2C1DC gets chharged when q1C2≠q2C1
AC gets charged in any conditionBC gets charged only when q1C2>q2C1CC gets charged only when q1C2<q2C1DC gets chharged when q1C2≠q2C1
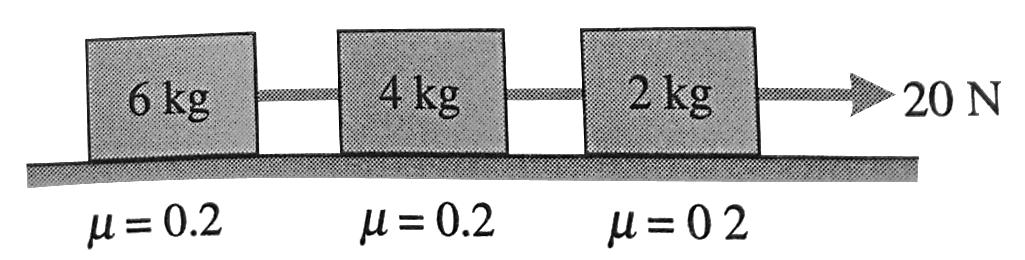
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. Friction force on 6 kg block is
View SolutionTwo capacitorsC1andC2=2C1 are connected in a circuit with a switch between them as showu in the figure- 3.302. Initially the switch is open and C1 holds charge Q. The switch is closed. In steady state, the charge on the two capacitors will be given as :
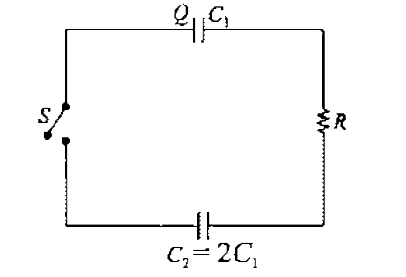
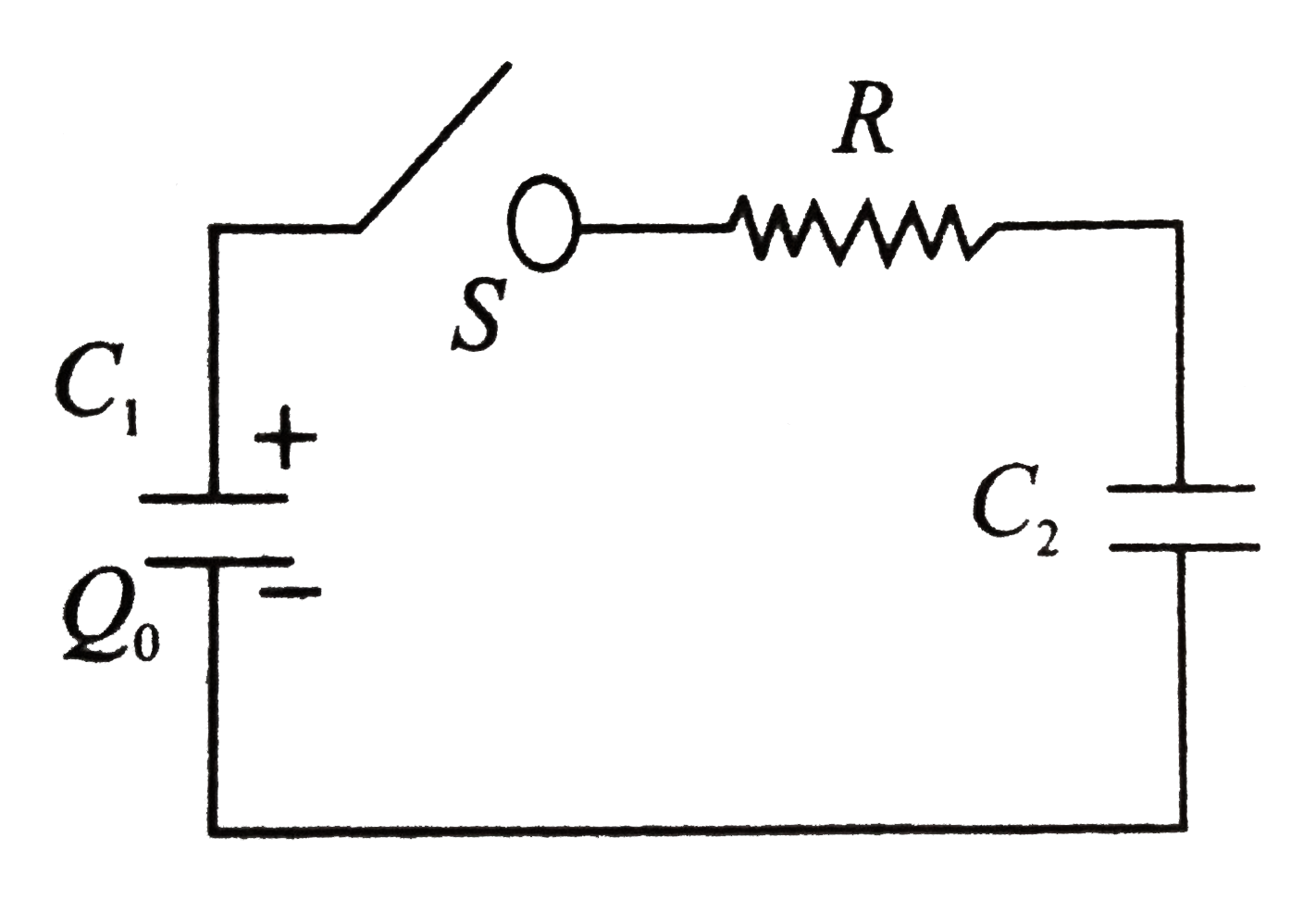
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
View SolutionTwo capacitorsC1andC2=2C1 are connected in a circuit with a switch between them as showu in the figure- 3.302. Initially the switch is open and C1 holds charge Q. The switch is closed. In steady state, the charge on the two capacitors will be given as :

View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is

View Solution
