A rope AB of linear mass density λ is placed on a quarter vertical fixed disc of radius R as shown in the figure. The surface between the disc and rope is rough such that the rope is just is equilibrium. Gravitational acceleration is g. Choose the correct option (s).

Coefficient of static friction between rope and disc is μ=1
Coefficient of static friction between rope and disc is μ=1√2
Maximum tension in the rope is at the top most point A of the rope
Maximum tension in the rope is λRg(√2−k1)
The correct Answer is:A, D
For equilibrium
λRg∫π20cosθdθ=μλRg∫π20sinθdθ
∴μ=1
At the position of maximum tension in the rope
λRdθgcosθ=μ(λRdθgsinθ)
∴θ=45∘
At any θ
dT=λRdθgcosθ−μλdθgsinθ
∫Tmax0dT=λRg∫π40(cosθ−sinθ)dθ
Tmax=λRg[sinθ+cosθ]π40=λRg[1√2+1√2−1]=λRg(√2−1)

Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
Knowledge Check
A unofrom rope of mass m is placeced on a smooth fixed sphere of radius R as shown in the figure .Find the tension T in the rope when it is in a horizontal plane at a vertical distance h=R/2 below the top of the sphere .
 Amg2πBmg2C√3mg2D√3mg2π
Amg2πBmg2C√3mg2D√3mg2πA solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).
 AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3
AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3A uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),
 Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR .
Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR .
A particle of mass 'm' is attached to the rim of a uniform disc of mass 'm' and radius R. The disc is rolling wihtout slipping on a stationery horizontal surface as shown in the figure. At a particular instant, the particle is at the topmost position and centre of the disc has speed v0 amd its angular speed is ω. Choose the correct option (s).
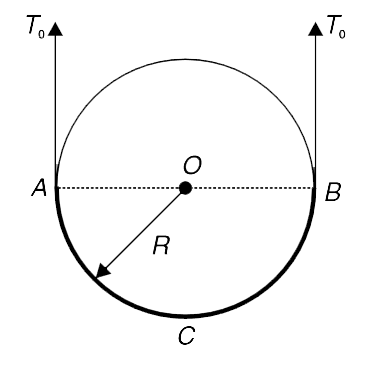
View SolutionA smooth cylinder is fixed with its axis horizontal. Radius of the cylinder is R. A uniform rope (ACB) of linear mass density λ (kg/m) is exactly of length πR and is held in semicircular shape in vertical plane around the cylinder as shown in figure. Two massless strings are connected at the two ends of the rope and are pulled up vertically with force T0 to keep the rope in contact with the cylinder.
(a) Find minimum value of T0 so that the rope does not lose contact with the cylinder at any point.
(b) If T0 is decreased slightly below the minimum value calculated in (a), where will the rope lose contact with the cylinder.
View SolutionA disc of radius R and mass M is under pure rolling under the action of a force F applied at the topmost point as shown in figure. There is sufficient friciton between the disc and the horizontal surface. The acceleration is given as

View SolutionA disc of radius R and mass M is under pure rolling under the action of a force F applied at the topmost point as shown in figure. There is sufficient friciton between the disc and the horizontal surface. The acceleration is given as

View SolutionA particle of mass 'm' is attached to the rim of a uniform disc of mass 'm' and radius R. The disc is rolling wihtout slipping on a stationery horizontal surface as shown in the figure. At a particular instant, the particle is at the topmost position and centre of the disc has speed v0 amd its angular speed is ω. Choose the correct option (s).
View Solution
