Graphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
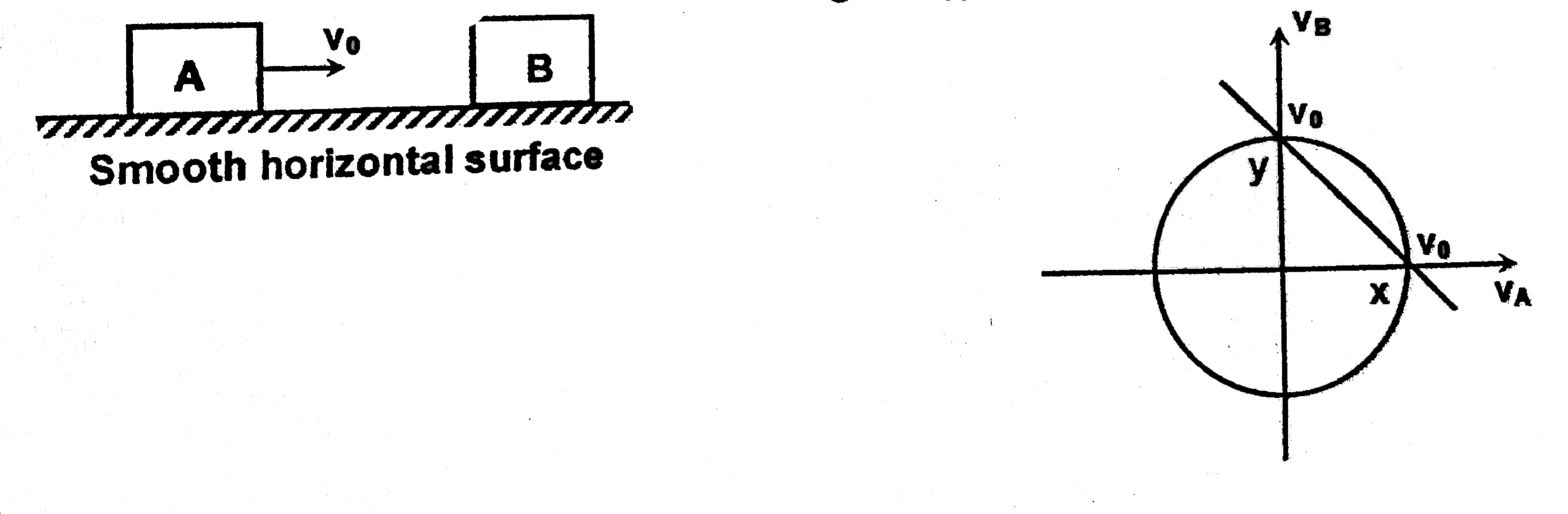
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is

12
1/3
1
Collision no possible
The correct Answer is:B
e=43−232=13
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
Graphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
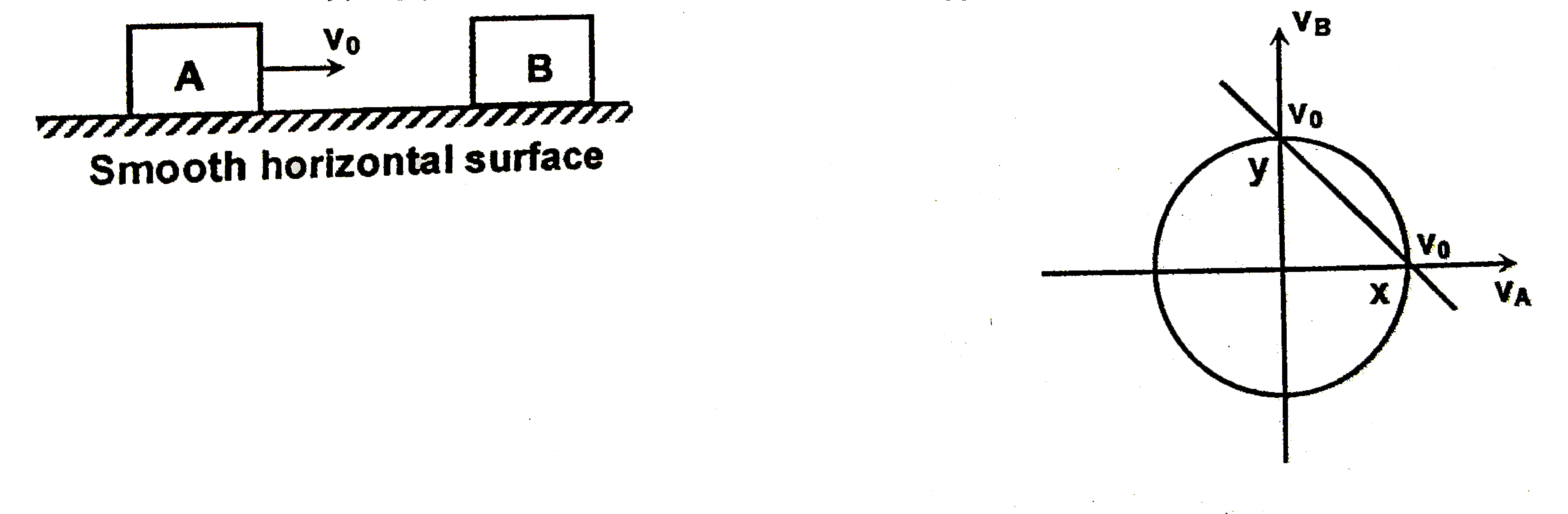
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
If the collision is perfectly inelastic, then the vA−vB plot is
View SolutionIf block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
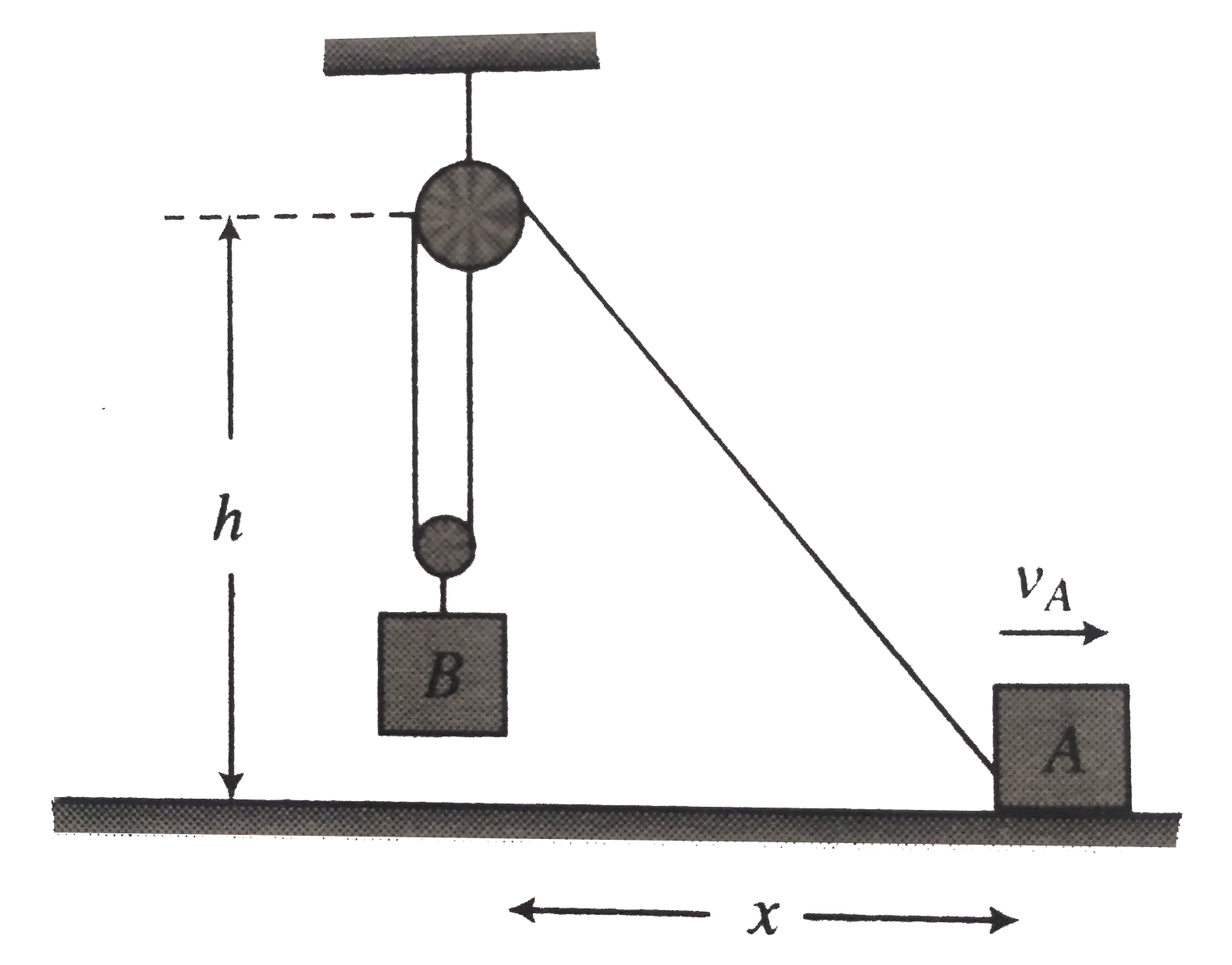
View Solution
Knowledge Check
Graphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.

So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
If the collision is perfectly inelastic, then the vA−vB plot isA B
B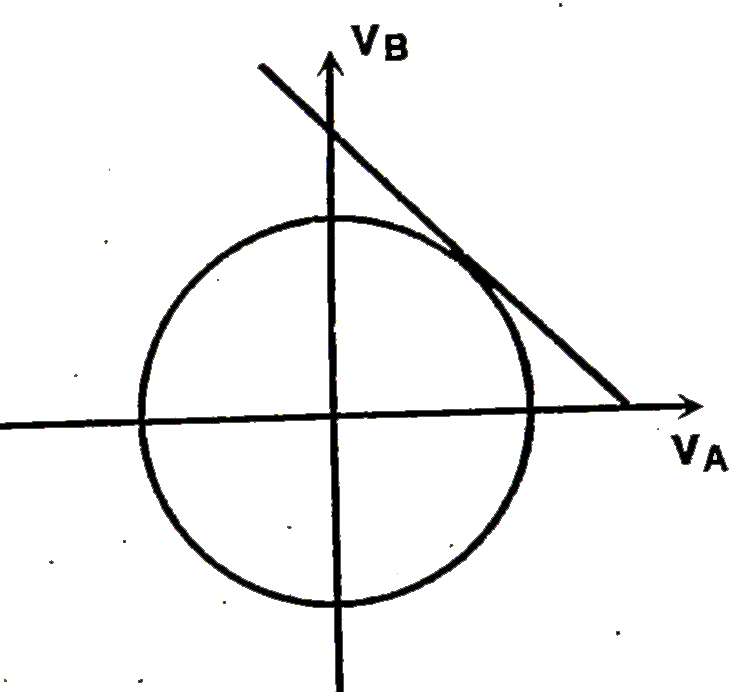 C
C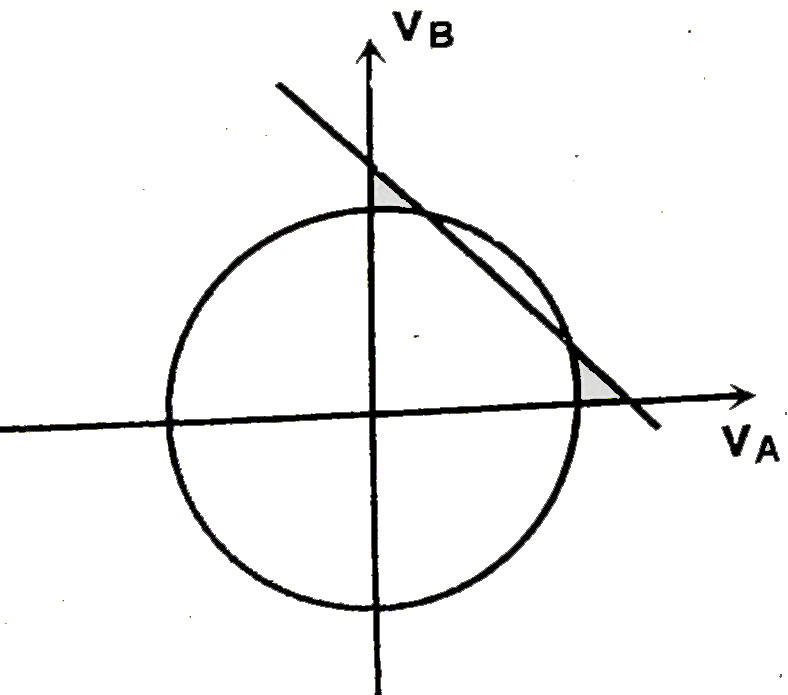 D
D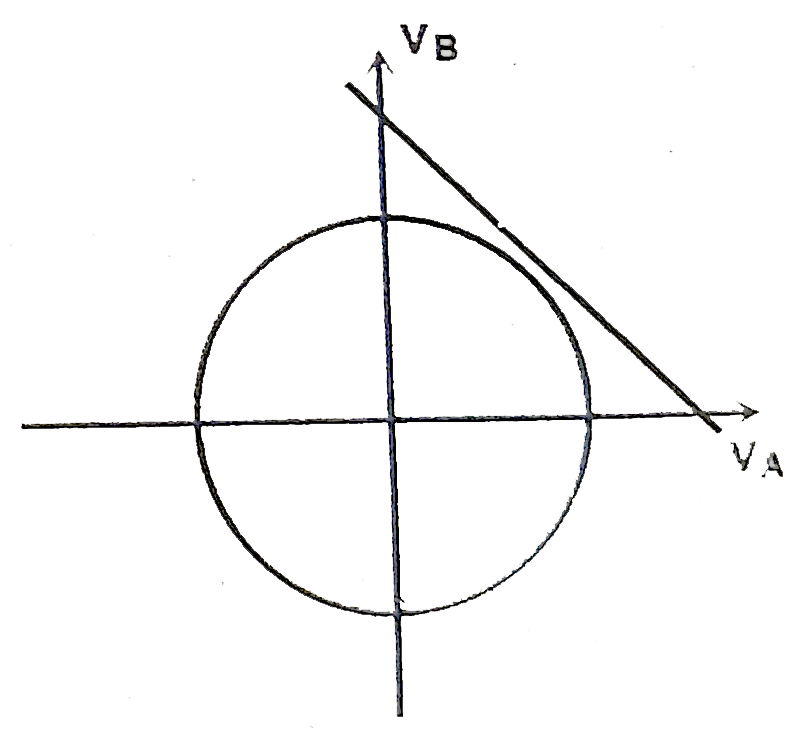
If block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
 AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2
AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2A block of mass m moving with speed v0 strikes another particle of mass 2m at rest. If collision is head - on and the coefficient of restitution e=1/2 , then the loss in kinetic energy will be
A12mv20B13mv20C23mv20D34mv20
A heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View Solution
