Let $A B C$ be a triangle right-angled at $A a n d S$ be its circumcircle. Let $S_{1}$ be the circle touching the lines $A B$ and $A C$ and the circle $S$ internally. Further, let $S_{2}$ be the circle touching the lines $A B$ and $A C$ produced and the circle $S$ externally. If $r_{1}$ and $r_{2}$ are the radii of the circles $S_{1}$ and $S_{2}$ , respectively, show that $r_{1} r_{2} = 4$ area $(A B C) .$

A

$\frac{r_{1} r_{2}}{4}$

B

$\frac{r_{1} r_{2}}{8}$

C

$\frac{r_{1} r_{2}}{2}$

D

$r_{1} r_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Equation of $S = {(x - \frac{a}{2})}^{2} + {(y - \frac{b}{2})}^{2} = \frac{a^{2} + b^{2}}{4}$
$x^{2} + y^{2} - a x - b y = 0$
And circle with centre $(r, r)$ and radius $r$
Touches $A B$ and $A C$ its equation is
${(x - r)}^{2} + {(y - r)}^{2} = r^{2}$
$x^{2} + y^{2} - 2 x r - 2 y r + r^{2} = 0$
Both circle touches internally or externally
Using $\sqrt{{(r - \frac{a}{2})}^{2} + {(r - \frac{b}{2})}^{2}} = \sqrt{(\frac{a^{2}}{4} + \frac{b^{2}}{4})} \pm r$
$Δ A B C = \frac{r_{1} r_{2}}{4}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

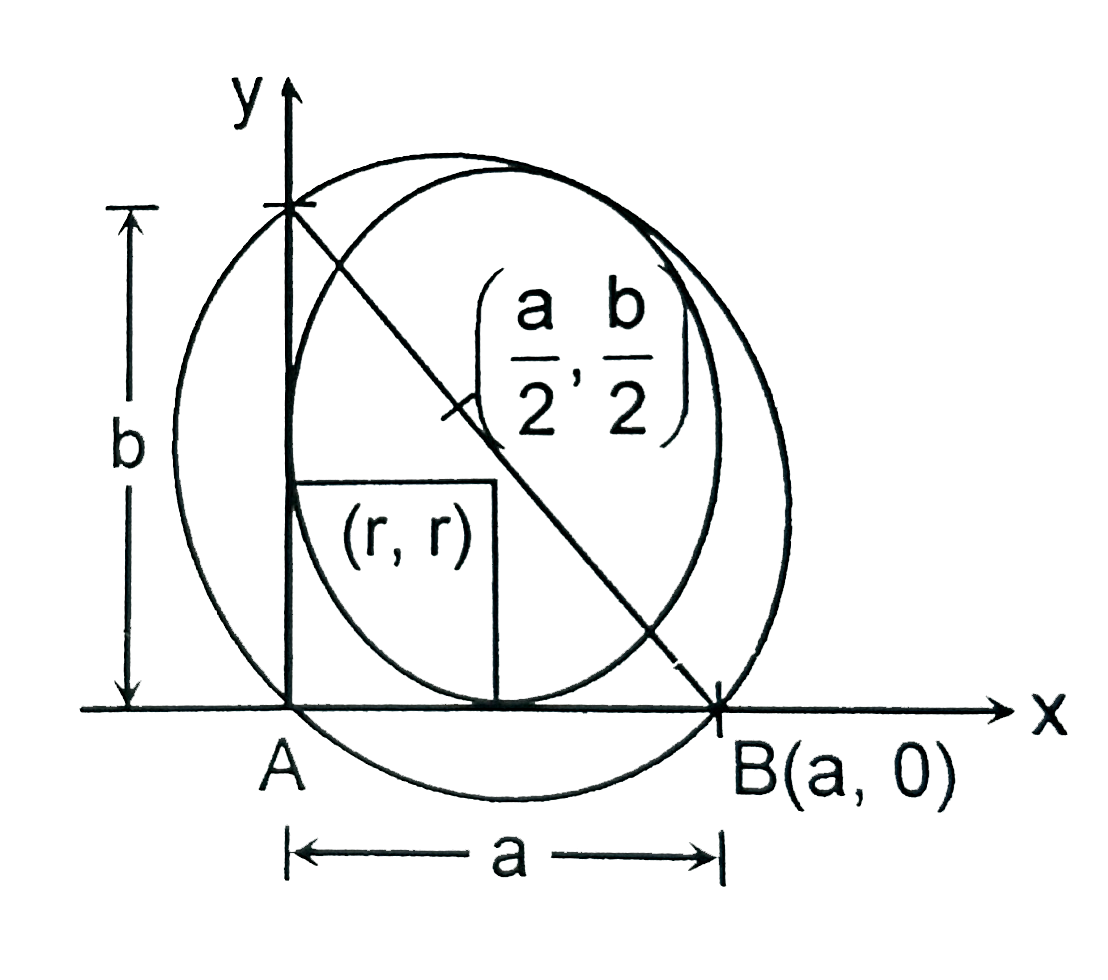
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A circle touches the line L and the circle $C_{1}$ externally such that both the circles are on the same side of the line, then the locus of centre of the circle is $:$
Aellipse
Bhyperbola
Cparabola
Dpart of straight line
Question 2 - Select One
IF two circles of radii $r_{1}$ and $r_{2}$ $(r_{2} > r_{1})$ touch internally , then the distance between their centres will be
A $r_{1} - r_{2}$
B $r_{2} - r_{1}$
C $r_{1}^{2} - r_{2}^{2}$
D $r_{2}^{2} - r_{1}^{2}$
Question 3 - Select One
Let ABCD be a square of side length 2 units. $C_{2}$ is the fircle through the vertices A, B, C, D and $C_{1}$ is the circle touching all the of the square ABCD. L is a lien through vertex A. A circle touches the line L and the circle $C_{1}$ externally such that both the circles are on the same side of the line L. The locus of the centre of the circle is
Aellipse
Bhyperbola
Cparabola
Dpair of straight lines

FIITJEE-TEST PAPERS-MATHEMATICS

Home
Ask Doubt
Profile