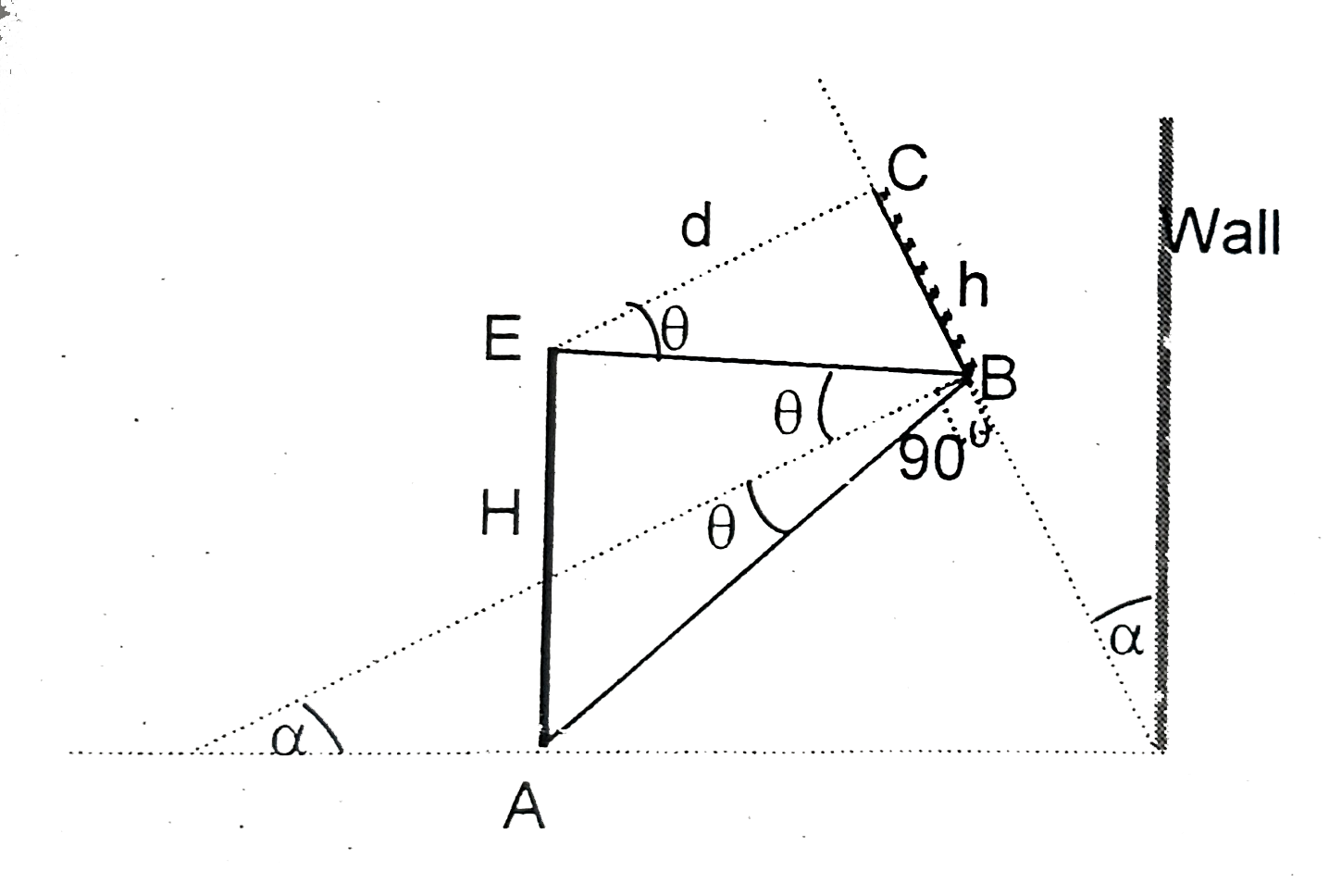
A man of height =3/2m,wants to see himself in plane mirror from top to bottom. The plane mirror is inclined with vertical wall at angle α=53∘. If the least size of mirror to see him 3nm, the distance of eye from mirror is d=3m, find the value of m
The correct Answer is:8
hd=tanθ
Using triangle EAB
dcosθsin{90−(α+θ)}=Hsin2θ
⇒dcos(α+θ)=H2sinθ
⇒2d=H[cosαcotθ−sinα]
=Hcosα(dh)−Hsinα
⇒h=Hdcosα2d+Hsiα=32×3×352×3+32×45=2736×2=38
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A man is standing at distance x from a plane mirror in front of him. He wants to see the entire wall in mirror which is at distance. y behind the man. Find the minimum size of the mirror required.
View SolutionA man of height 1.4 m wishes to see his full image in a plane mirror placed at distance of 2 m . the minimum height of the mirror should be
View Solution
Knowledge Check
A man of height 1.6 m wishes to see his full image in a plane mirror. The minimum height of the mirror needed for this purpose is
A3.2 mB2.4 mC1.6 mD0.8 mA man of height 1.6 m wishes to see his full image in a plane mirror placed at a distance of 2 m. The minimum length of the mirror should be
A0.4 mB0.8 mC1.6 mD2.4 mA concave mirror of focal length produces an image m times the size of the object. If image is real, then the distance of the object from mirror is
A(m+1)fB(m+1m)fC(m−1m)fDmf
How many image can a man see if he stands between two plane mirrors inclined at an angle of 60∘ ?
View SolutionA man of height 170cmwants to see his complete image in a plane mirror(while standing).His eyes are at a height of 160cmfrom the ground.
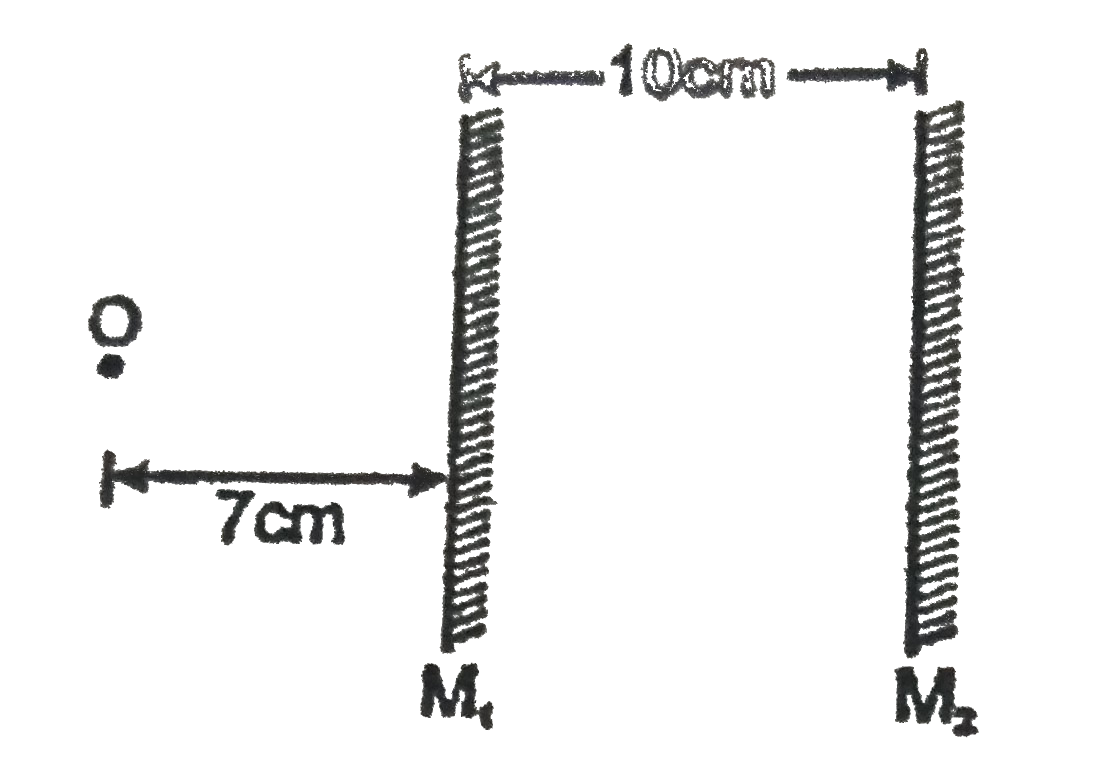
View SolutionThe figure shows two parallel plane mirrors placed 10cm apart. An object O is placed 7cm from mirror M1. Then the distance of final image formed from mirror M1 is:
View SolutionTwo plane mirrors are inclined at an angle θ to one another A ray of light incident on the first mirror and parallel ot the second mirror is reflected from the second mirror parallel to the first mirror ,
What is the value of θ
View SolutionA pole of height 1 . 8 m stands in front of a larger vertical plane mirror . The distance of the image from the pole at a distance of 1 . 5 m from the mirror is
View Solution
