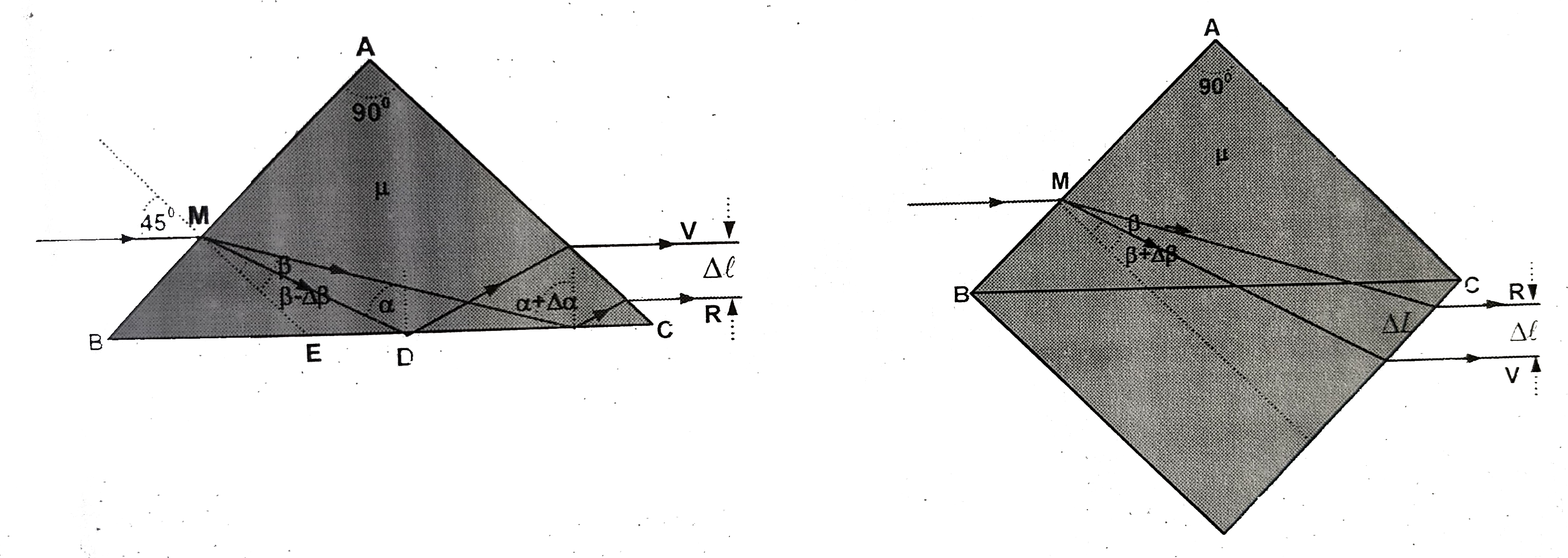
ABC is an isosceles right angled triangular refecting prism of average refractive index μ. When incident rays on face AB are paralel to face BC, then they emerges from Face AC, which are also parallel to Face BC as shown in figure-I. The prims capable to do so, known as Dove Prism. In figure II, the Dove Prism is used for dispersion of incident light containing red colour and violet colour only. The red colour and violet colour lights are separated (displaced) on screen by a distance Δl. In reality, each ray of any colour has some width, whcih can be designated as d. It is clear that an observer candistinguish the red and violet rays that emerges from prism only if Δl≥d. Otherwise the bundles of rays will overlap and mix.
[Given for Dove Prism in figure II: μR=√52,Δμ=μV−μR=0.02,√5=2.25,EF1m and AB=4cm]
![ABC is an isosceles right angled triangular refecting prism of average refractive index mu. When incident rays on face AB are paralel to face BC, then they emerges from Face AC, which are also parallel to Face BC as shown in figure-I. The prims capable to do so, known as Dove Prism. In figure II, the Dove Prism is used for dispersion of incident light containing red colour and violet colour only. The red colour and violet colour lights are separated (displaced) on screen by a distance Deltal. In reality, each ray of any colour has some width, whcih can be designated as d. It is clear that an observer candistinguish the red and violet rays that emerges from prism only if Deltalged. Otherwise the bundles of rays will overlap and mix. [Given for Dove Prism in figure II: mu(R)=sqrt(5/2),Deltamu=mu(V)-mu(R)=0.02, sqrt(5)=2.25, EF1m and AB=4cm] Choose the INCORRECT option](https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIT_JEE_PT3_P2_E01_317_Q01.png)
Choose the INCORRECT option
As per figure-I, the average refractive index of Dove Prism may be greater than 1
As per figure I the average refractive index of Dove Prism may be greater than √2
As per figure II ,the displacement Δl depends upon average refractive index μ and length of AB
As per figure II, he displacement Δl depends upon average refractive index μ and length of EF
The correct Answer is:D
In figure -I, total internal reflection take place at face AB.
∠EMD+∠MDE=∠BEM
⇒β(90−α)=45∘
⇒sin(β+45∘)>(1μ)
⇒sinβ+cosβ>√2μ……….(1)

According to law of refraction at point M, we can write
1×sin(45∘)=μsinβ⇒sinβs=1μ√2⇒cosβ=√1−12μ2
Putting these value in equation (1), we have
1μ√2+√1−12μ2>√2μ⇒√2μ2−1>1⇒μ>1
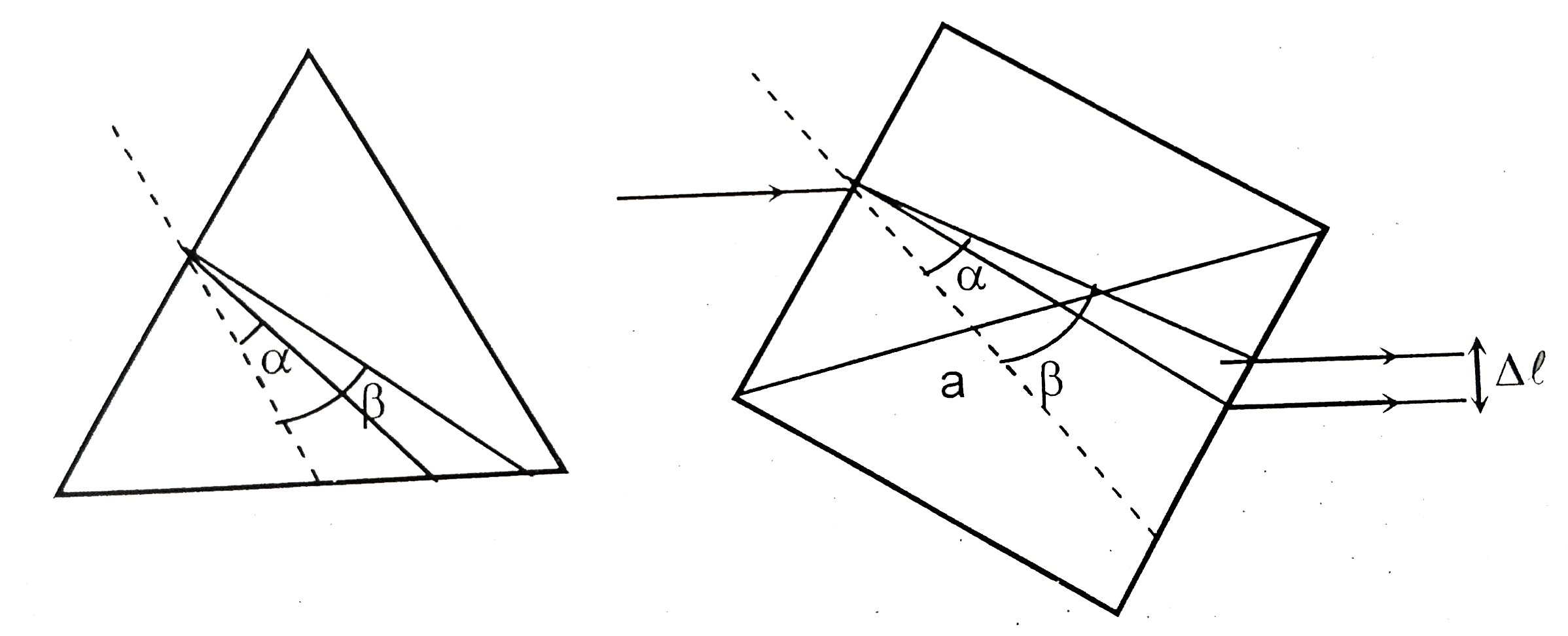
In figure II: Replace the Dove Prism, by glass cube of side as AB
Δl=ΔL√2.............(2)
From geometry, we can write
sinβ=1μR√2 and sin(β−Δβ)=1(μR+ΔμR)√2
ΔL=atanβ−atan(β−Δβ)=1√2μ2R−1−a√2(μ∣r+Δμ)2−1
⇒Δ=a√2μ2R−1⎛⎜⎝1−
⎷2μ2R−12(μR+Δμ)2−1⎞⎟⎠=a√μ2R−1⎛⎜⎝1−
⎷2μ2R−12(μR+Δμ)2−1⎞⎟⎠
⇒ΔL=a√2μ2R−1⎛⎜
⎜⎝1−√2μ2R−12μ2R+4μRΔμ+2(Δμ)2−1⎞⎟
⎟⎠
Neglecting the value (Δμ)2, we have
⇒Δ=a√2μ2R−1⎛⎜
⎜
⎜⎝1−
⎷11+4μRΔμ2μ2R−1⎞⎟
⎟
⎟⎠−a√2m2R−1⎛⎜⎝1−{1+4μRΔμ2μ2R−1}−12⎞⎟⎠
Expand binomially, we have
⇒ΔL=2aμRΔμ(2μ2R−1)32
Putting this value in equation (2), we have
Δl=√2aμRΔμ(2μ2R−1)32
Second method:
ΔL=(ddβ(atanβ))×Δβ
ΔL=(asec2β)×Δβ
Also sinβ=1√2μR
⇒cosβΔβ=1√2μ2RΔμ
⇒ΔL=asec2β×Δμ√μ2Rcosβ
⇒ΔL=2aμRΔμ(2μ2Rcosβ)
Third method:
Δl=ΔL√2,sinα=1μr√2,sinβ=1μv√2
ΔL=atanα=atanβ
=[1√2μ2r−1−1√2μ2v−1]
=a[12−12√1+μrΔμ]
=a2[a−(1+μrΔμ)−1/2]
=a2[1−1+12μrΔμ]
=a4μrΔμ
Δl=ΔL√2=a4√2μrΔμ=4cm4√2×√5√2×2100
=√5100cm=√5×10−4m
=2.25×10−4m
Since : Δl≥d
⇒d≤2.25×10−4m
√2μ2v−1=√2(μr+Δμ)2−1
⇒√4+4μrΔμ[(Δμ)2≈0]
=2√1+μrΔμ
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A ray of light the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism. Given angle of prism is A.
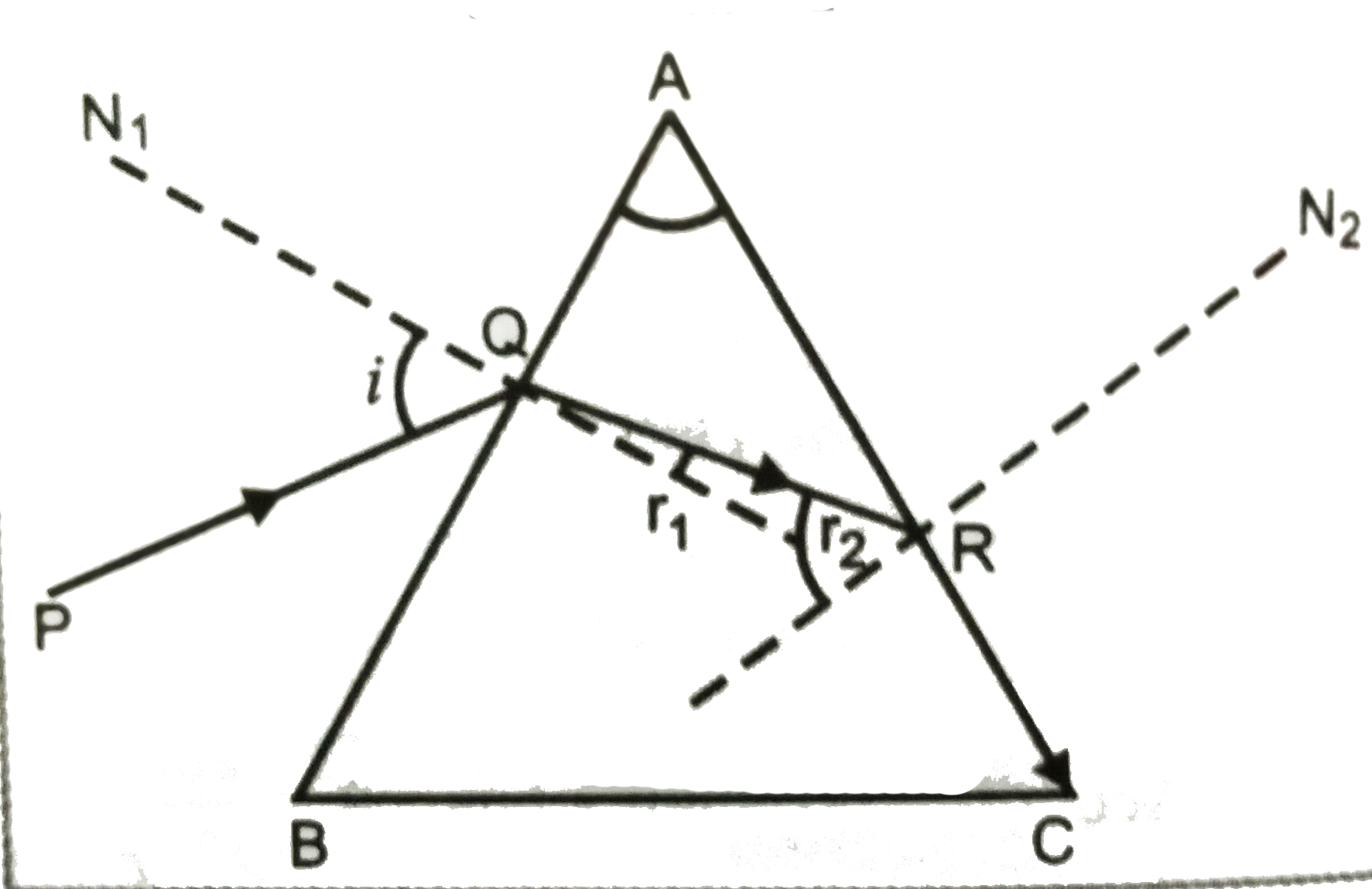
View SolutionA ray of light enters the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism, given angle of prism is A.
View Solution
Knowledge Check
ABC is an isosceles right angled triangular refecting prism of average refractive index μ. When incident rays on face AB are parallel to face BC, then they emerges from Face AC, which are also parallel to Face BC as shown in figure-I. The prims capable to do so, known as Dove Prism. In figure II, the Dove Prism is used for dispersion of incident light containing red colour and violet colour only. The red colour and violet colour lights are separated (displaced) on screen by a distance Δl. In reality, each ray of any colour has some width, which can be designated as d. It is clear that an observer candistinguish the red and violet rays that emerges from prism only if Δl≥d. Otherwise the bundles of rays will overlap and mix.
[Given for Dove Prism in figure II: μR=√52,Δμ=μV−μR=0.02,√5=2.25,EF1m and AB=4cm]

Find the maximum value of width d of bundle of rays that can be resolved at the outlet of Dove Prism as shown in the figureIIA2.25×10−3mB22.25×10−4mC1.125×10−3mD1.125×10−4mABC is an isosceles right angled triangular reflecting prism of average refractive index μ . When incident rays on face AB are parallel to face BC , then they emerges from Face AC . which are also parallel to Face BC as shown in figure-l. The prism capable to do so , known as Dove Prism. In figure-ll, the Dove Prism is used for dispersion of incident light containing red colour and violet colour only. The red colour and violet colour lights are separated( displaced ) on screen by a distance Af. In reality , each ray of any colour has some width, which can be designated as d. It is clear that an observer can distinguish the red and violet rays that emerges from prism only if Δφ≥d .Otherwise the bundles of rays will overlap and mix.
Q . Choose the INCORRECT option.
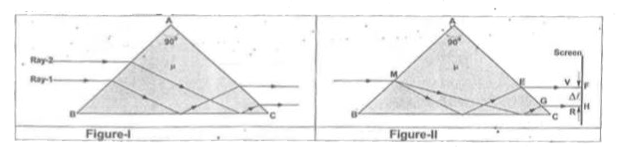 AAs per figure-l, the average refractive index of Dove Prism may be greater than 1.BAs per figure-l, the average refractive index of Dove Prism may be greater than√2CAs per figure-ll, the displacement depends upon average refractive indexμ and length of AB. ,DAs per figure-ll, the displacement M depends upon average refractive indexμ and length of EF
AAs per figure-l, the average refractive index of Dove Prism may be greater than 1.BAs per figure-l, the average refractive index of Dove Prism may be greater than√2CAs per figure-ll, the displacement depends upon average refractive indexμ and length of AB. ,DAs per figure-ll, the displacement M depends upon average refractive indexμ and length of EFABC is an isosceles right angled triangular reflecting prism of average refractive index μ . When incident rays on face AB are parallel to face BC , then they emerges from Face AC . which are also parallel to Face BC as shown in figure-l. The prism capable to do so , known as Dove Prism. In figure-ll, the Dove Prism is used for dispersion of incident light containing red colour and violet colour only. The red colour and violet colour lights are separated( displaced ) on screen by a distance Af. In reality , each ray of any colour has some width, which can be designated as d. It is clear that an observer can distinguish the red and violet rays that emerges from prism only if Δφ≥d .Otherwise the bundles of rays will overlap and mix.
Q Find the maximum value of width d of bundle of rays that can be resolved at the outlet of Dove Prism as shown in the figure-ll.
 A2.25×10−3mB2.25×10×−4mC1.125×10−3D1.125×10−4m
A2.25×10−3mB2.25×10×−4mC1.125×10−3D1.125×10−4m
An isosceles prism has one of the refracting surfaces silvered. A ray of light is incident normally on the refracting face AB. After two reflections, the ray emerges from the base of the prism perpendicular to it. Find the angle of the prism.
View SolutionAn isosceles prism has one of the refracting surfaces silvered. A ray of light is incident normally on the refracting face AB. After two reflections, the ray emerges from the base of the prism perpendicular to it. Find the angle of the prism.
View SolutionIf a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
View SolutionLight enters an isosceles right triangular prism at normal incidence through face AB and undergoes total internal reflection at face BC as shown below.
The minimum value of the refractive index of the prism is close to
View SolutionIf a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
View Solution
