The vertices of a triangle are and . The points and divide the sides and in the ratio respectively. Another point is taken in space such that the perpendicular drawn from to the plane containing , meets the plane at the point of intersection of the line segments and . If the distance of from plane of triangle is , units, ten
the volume of the tetrahdron is cubic units
the volume of the tetrahedron is cubic units
one of the equation of the line is
one of the equuation of the line is
The correct Answer is:A, C
Area of tetrahedron
(Area of base triangle) height cubic units
units
. of of
of
Vector equation of is
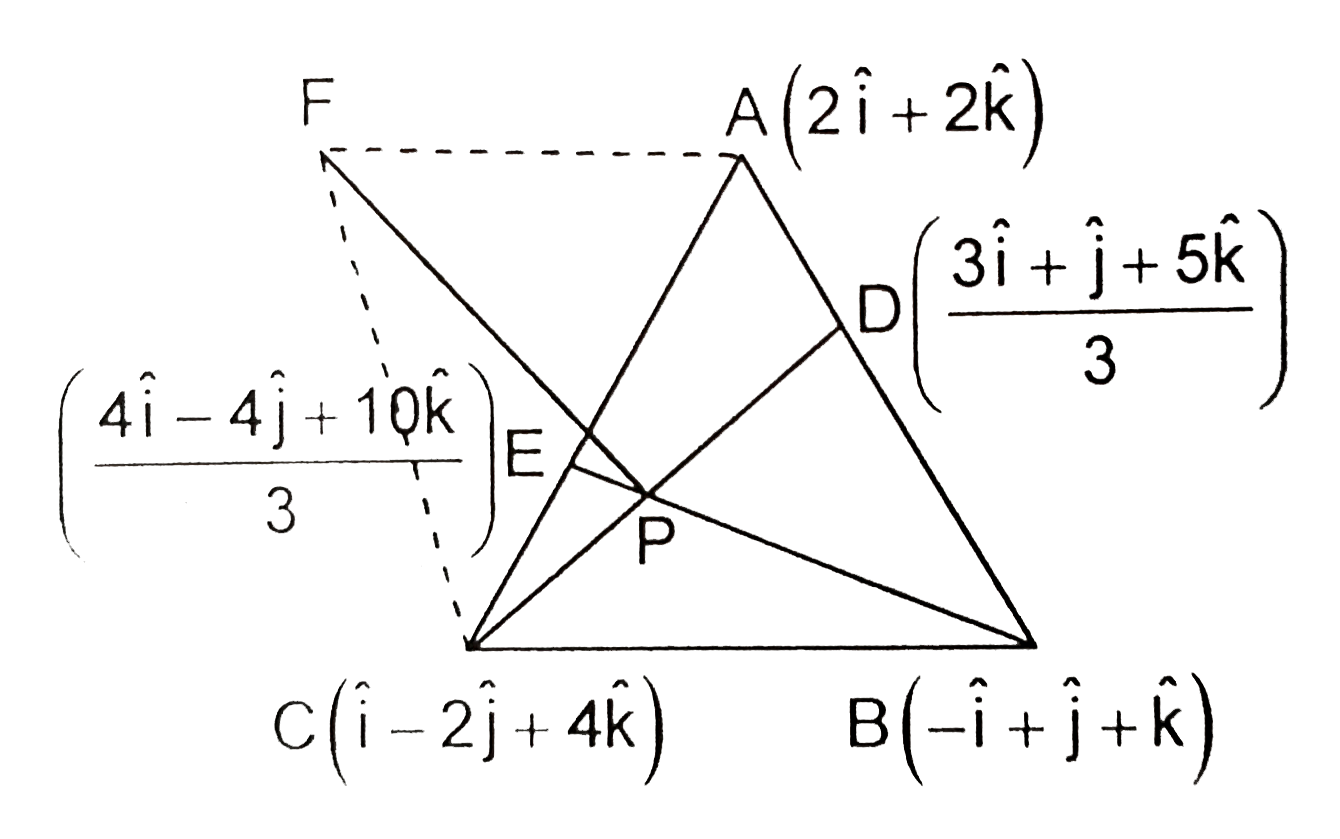
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABC is a triangle with vertices A(-1,4), B(6,-2) and C(-2,4). D, E and F are the points which divide each AB, BC and CA, respectively in the ratio 3:1 internally. Then, the centroid of the △DEF is
A(3,6)B(1,2)C(4,8)D(-3,6)The vertices of a triangle an A(1,2),B(−1,3) and C(3, 4). Let D, E, F divide BC, CA, AB respectively in the same ratio.
Statement I : The centroid of triangle DEF is (1, 3).
Statement II : The triangle ABC and DEF have the same centroid.AStatement I is true, Statement II is true, Statement II is a correct explanation for Statement I.BStatement I is true, Statement II is true, Statement II is not a correct explanation for Statement I.CStatement I is true, Statement II is false.DStatement I is false, Statement II is true.
Thevertices of a triangle ABC are A(−7,8),B(5,2)andC(11,0). If D, E, F are the mid-points of the sides BC,CAandAB respectively, show that ΔABC=4ΔDEF.
View SolutionIf D(2,1,0),E(2,0,0) and F(0,1,0) are mid points of the sides BC,CA and AB of triangle ABC respectively, then the centroid of triangle ABC is
View SolutionThe points D,E,F divide BC,CAandAB of the triangle ABC in the ratio 1:4,3:2and3:7 respectively and the point divides AB in the ratio 1:3, then (¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF):¯¯¯¯¯¯CK is equal to
View SolutionThe vertices of a triangle an A(1,2),B(−1,3) and C(3, 4). Let D, E, F divide BC, CA, AB respectively in the same ratio.
Statement I : The centroid of triangle DEF is (1, 3).
Statement II : The triangle ABC and DEF have the same centroid.
View SolutionIf D(3,-2) , E(-3,1) and F(4,-3) are the mid-points of the sides BC, CA and AB respectively of ΔABC , find the co-ordinates of point A , B and C .
View SolutionIf D(3,-2) , E(-3,1) and F(4,-3) are the mid-points of the sides BC, CA and AB respectively of ΔABC , find the co-ordinates of point A , B and C .
View Solution
