Let the equation of a straight line $L$ in complex form be $a ¯ z + ¯ a z + b = 0$ , where is a complex number and $b$ is a real number then

the straight line $\frac{z - c}{a} + \frac{i (¯ z - ¯ c)}{a} = 0$ makes a angle of $45^{\circ}$ with $L$ and passed through a point $c$ (where $c$ is a complex number)

the straight line $\frac{z - c}{a} = \frac{i (¯ z - ¯ c)}{¯ a}$ makes an angle of $45^{\circ}$ with $L$ and passes through $a$ and $c$ (where $c$ is a complex number)

the complex slope of the line $L$ is $- \frac{a}{a}$

the complex slope of the line $L$ is $\frac{a}{a}$

Text Solution

Verified by Experts

The correct Answer is:A, B, C

Let $P (z)$ be any point on the required line.
Then, $\frac{- - \to C P}{∣ ∣ \to C P ∣ ∣}$ i.e. $\frac{z - c}{| z - c |}$ is a unit vector parallel to it
Let $A (z_{1})$ and $B (z_{2})$ be two points on
$¯ a z + a ¯ z + b = 0$ then $\frac{z_{2} - z_{1}}{| z_{2} - z_{1} |}$ is a unit vector parallel to the line
$a ¯ z + ¯ a z + b = 0$
$\frac{z - c}{| z - c |} = \frac{z_{2} - z_{1}}{| z_{2} - z_{1} |} e^{\pm i (\frac{π}{4})}$
$\frac{{(z - c)}^{2}}{(z - c) (¯ z - ¯ c)} = \frac{{(z_{2} - z_{1})}_{2}^{2}}{(z_{2} - z_{1}) ({¯ z}_{2} - {¯ z}_{1})} e^{\pm i \frac{π}{2}}$
$(\frac{z - c}{¯ z - ¯ c}) = \pm i (\frac{z_{2} - z_{1}}{{¯ z}_{2} - {¯ z}_{1}})$ .......(1)
$∵ A (z_{1}$ and $B (z_{2})$ are on the line $a ¯ z + ¯ a z + b = 0$ therefore $a {¯ z}_{1} + ¯ a z_{1} + b = 0$
$a {¯ z}_{2} + ¯ a z + b = 0$
$\Rightarrow - \frac{a}{a} = \frac{z_{2}}{{¯ z}_{2}} = (\frac{z_{2} - z_{1}}{{¯ z}_{2} - {¯ z}_{1}})$ ......(2)
From equation (1) and (2) we get $\frac{z - c}{a} \pm \frac{i (¯ z - ¯ c)}{¯ a} = 0$

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

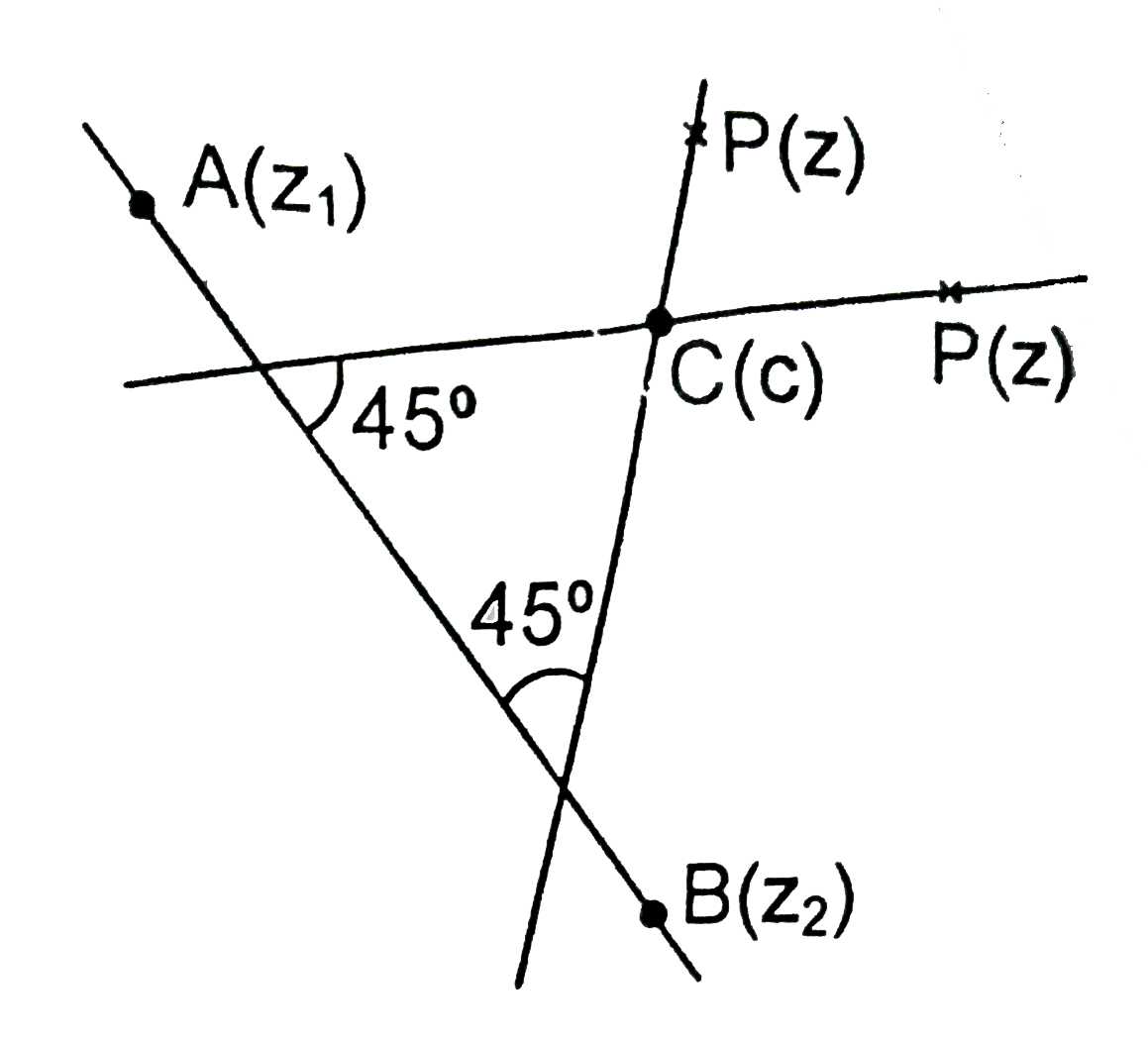
Topper's Solved these Questions

Knowledge Check

An equation of straight line joining the complex numbers a and ib (where a, b $ε$ R and a, b $\neq$ 0) is
A $z (\frac{1}{a} - \frac{i}{b}) + ¯ z (\frac{1}{a} + \frac{i}{b}) = 2$
B $z (\frac{1}{a} - \frac{i}{b}) + ¯ z (\frac{1}{a} + \frac{i}{b}) = 2$
C $z (a + i b) + ¯ z (a - i b) = 2 a b$
DNone of these
The equation $¯ b z + b ¯ z = c$ , where b is a non-zero complex constant and c is a real number, represents
Aa circle
Ba straight line
Ca pair of straight line
Dnone of these
Consider the equaiton of line $a ¯ z + a ¯ z + a ¯ z + b = 0$ , where b is a real parameter and a is fixed non-zero complex number.
The intercept of line on real axis is given by
A $\frac{- 2 b}{a + ¯ a}$
B $\frac{- b}{2 (a + ¯ a)}$
C $\frac{- b}{a + ¯ a}$
D $\frac{b}{a + ¯ a}$

FIITJEE-TEST PAPERS-MATHEMATICS

Home
Ask Doubt
Profile

Let the equation of a straight line L in complex form be a¯z+¯az+b=0, where is a complex number and b is a real number then

The correct Answer is:A, B, C

Topper's Solved these Questions

Similar Questions

Knowledge Check

An equation of straight line joining the complex numbers a and ib (where a, b ε R and a, b ≠ 0) is

The equation ¯bz+b¯z=c, where b is a non-zero complex constant and c is a real number, represents

Consider the equaiton of line a¯z+a¯z+a¯z+b=0, where b is a real parameter and a is fixed non-zero complex number. The intercept of line on real axis is given by

FIITJEE-TEST PAPERS-MATHEMATICS

Let the equation of a straight line $L$ in complex form be $a ¯ z + ¯ a z + b = 0$ , where is a complex number and $b$ is a real number then

An equation of straight line joining the complex numbers a and ib (where a, b $ε$ R and a, b $\neq$ 0) is

The equation $¯ b z + b ¯ z = c$ , where b is a non-zero complex constant and c is a real number, represents

Consider the equaiton of line $a ¯ z + a ¯ z + a ¯ z + b = 0$ , where b is a real parameter and a is fixed non-zero complex number.
The intercept of line on real axis is given by