In the equation . Where is the two digit number whose value is and letters and each represents different and is as large as possible
A five digit number is made using digits (repetition not allowed), then which of the following is incorrect
A
probability that number made is divisible by 5 is
B
probability that number made is divisible by is
C
probability that number made is divisible by 4 is
D
probability that number made is divisible by 4 is
Text Solution
The correct Answer is:D
Set
Total numbers divisible by
Total numbers divisible by
Total number divisible by
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the equation A+B+C+D+E=FG. Where FG is the two digit number whose value is 10F+G and letters A,B,C,D,E,F and G each represents different and FG is as large as possible
If a five digit number is made using the digits A,B,C,D,E without repetition tenAthe probability that the number is divisible by 11 is 25Bthe probability that the number is divisible by 11 is 15Cthe probability that the number is divisible 4 is 14Dthe probability that the number is divisible by 4 is 25If a,b,c,d,e,f, g are in contiued proportion, then the value of a.b.c.e.f.g is
Ad3Bd7Cd6DNone of theseLet a, b, c, d, e be natural numbers in an arithmetic progression such that a + b + c + d + e is the cube of an integer and b + c + d is square of an integer. The least possible value of the number of digits of c is
A2B3C4D5
Find the values of A,B,C,D,E,F,G in the following
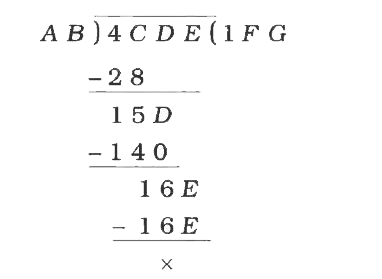
View SolutionIf f(x)=(log)e(1−x)and g(x)=[x] , then determine each of the following function :fg
View SolutionIf fandg are one-one functions, then a. f+g is one one b. fg is one one c. fog is one one d. no≠ofthese
View SolutionFind number of seven-digit number in the form of abcdefg(g,f,e, etc. Are digits at units, tens hundreds place etc.) where a<b<c<d>e>f>g.
View Solutionabcde is a five digit number when multiplied by 13 it gives a number, purely formed by the digit 9. Then the value of a+b+c+d+e is :
View Solution