Question

List-I gives different lens configurations. The radius of curvature of each surface is R. Rays of light parallel to the axis of lens from left of lens traversing through the lens get focused at distance f from the lens. List-II gives corresponding values of magnitudes of f (mu represent refractive index):-

Options

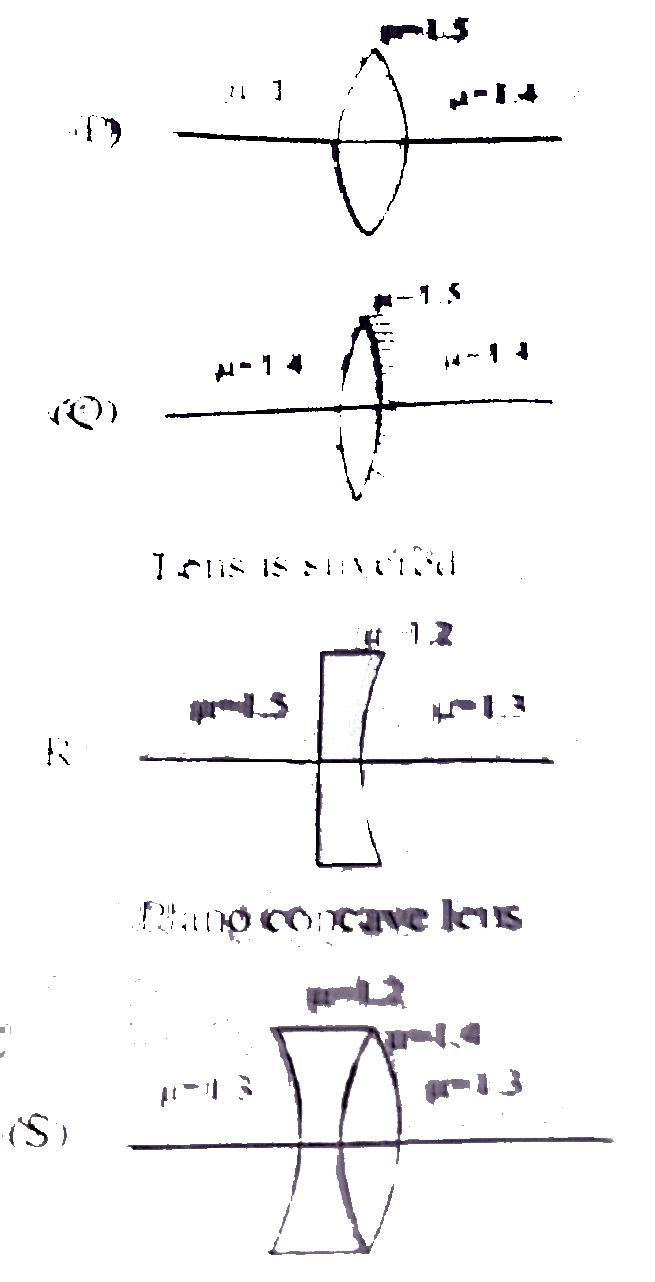
A. `{:(P,Q,R,S),(1,3,2,4):}`
B. `{:(P,Q,R,S),(1,2,3,4):}`
C. `{:(P,Q,R,S),(2,3,4,1):}`
D. `{:(P,Q,R,S),(3,4,1,2):}`

Answer

D

Explanation

`(P) (mu_(s)^('))/(v)-(mu_(s))/(u)=(mu_(L)-mu_(s))/(R_(1))-(mu_(L)-mu_(s)^('))/(R_(2))`
`(1)/(f)=(mu_(L)-mu_(s))/(mu_(s)^(')R_(I))-(mu_(L)-mu_(s)^('))/(mu_(s)^(')R_(2))`
`(1)/(f)=(1)/(R)[(1.5-1.0)/(1.4)+(1.5-1.4)/(1.4)]`
`(1)/(f)=(1)/(1.4R)[0.5+0.1]`
`(1)/(f)=(6)/(14R)=(3)/(7R)`
`f=(7R)/(3)`
`(Q) (1)/((f_(eq))_(m))= (1)/(f_(m))-(2)/(f_(L))=-(2)/(R)-(2)/(f_(L))`
`(1)/(f_(L))=((mu_(L))/(mu_(s))-1)(2)/(R)=(1.5/(1.4)-1)(2)/(R)=(0.1)/(1.4)xx(2)/(R)`
`(1)/(f_(L))=(1)/(7R)`
`(1)/((f_(eq))_(m))=-(2)/(R)-(2)/(7R)=-(16)/(7R)`
`implies (f_(eq))_(m)=-(7R)/(16)`

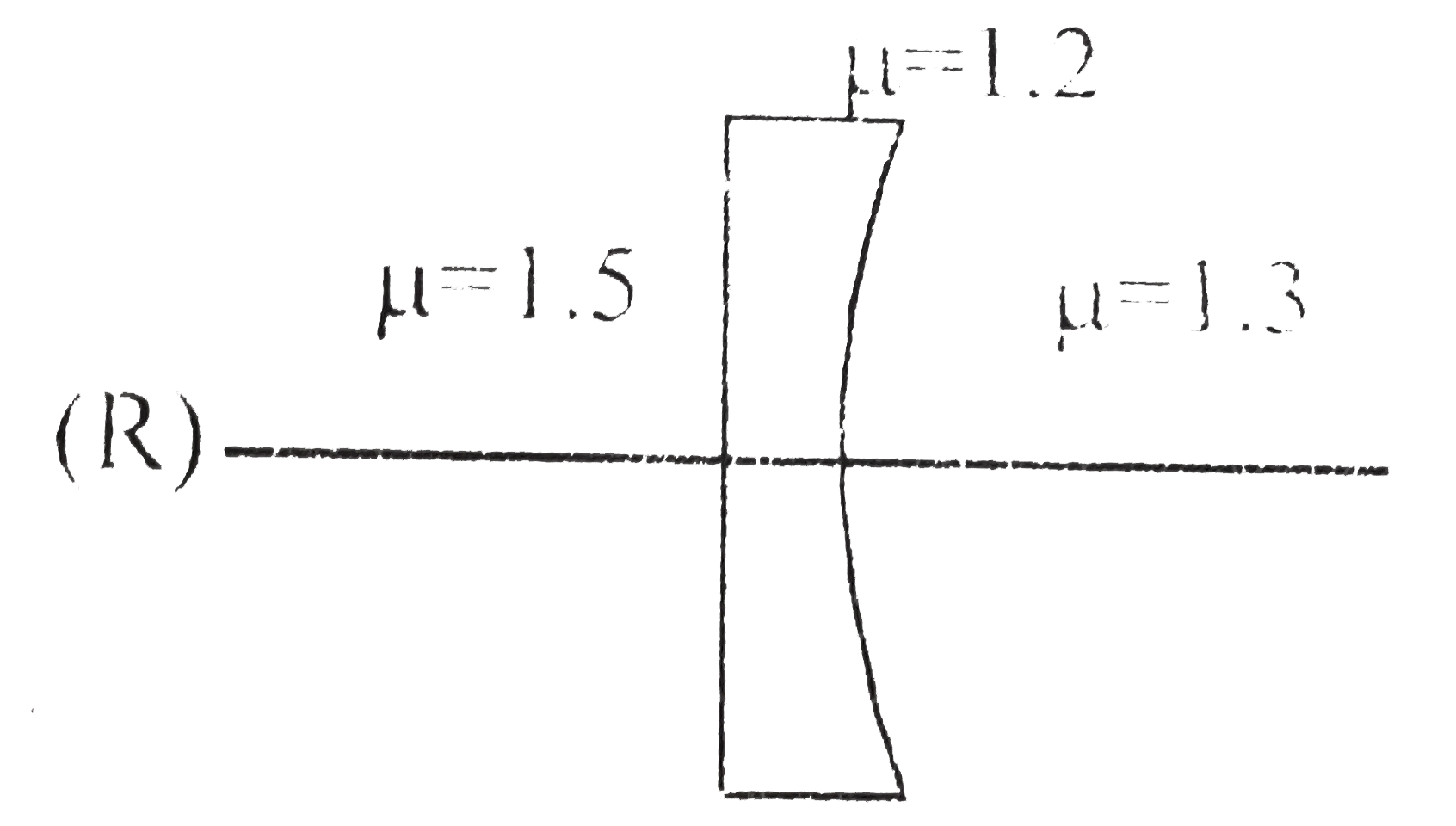
`(1)/(f)= [(1.2-1.5)/(1.3xxoo)-((1.2-1.3))/(1.3xxR)]`
`(1)/(f)=(1)/(13R)`
`(S) = 13R`
`(1)/(f_(1))=((1.2)/(1.3)-1)(-(2)/(R))=+(0.1)/(1.3)((2)/(R))=(2)/(13R)`
`(1)/(f_(2))=((1.4)/(1.3)-1)((2)/(R))=(2)/(13R)`
`(1)/(f_(eq))=(1)/(f_(1))+(1)/(f_(2))=(4)/(13R)`
`(1)/(f_(eq))=(13R)/(4)`