An optical fiber has index of refraction n=1.40 and diameter d=100μm. It is surrounded by air. Light is sent into the fiber along the axis as shown in figure. If smallest outside radius R permitted for a bend in the fiber for no light to escape is given by 50x(inμm) fill value of x.

The correct Answer is:7
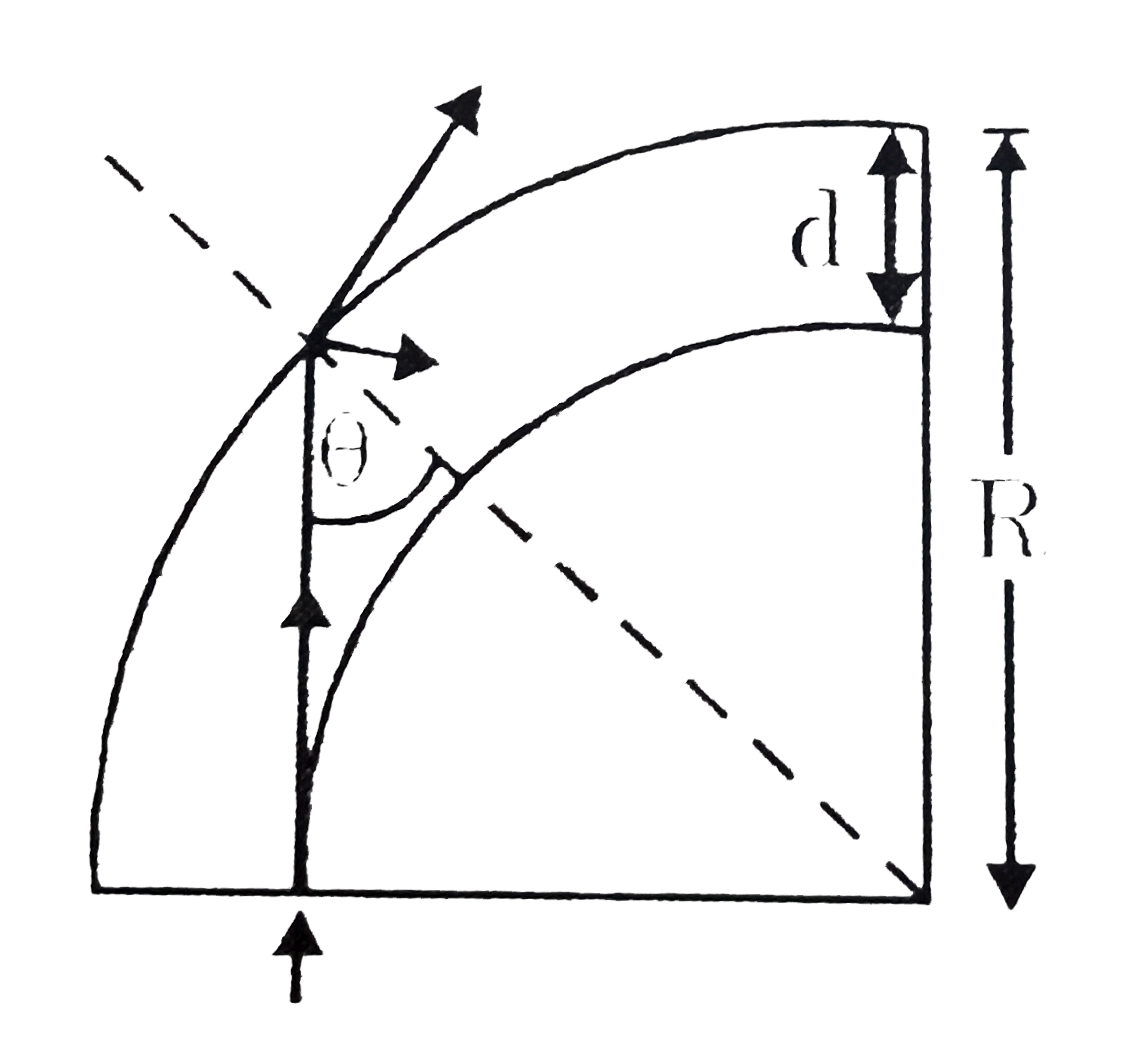
A ray along the inner edge will escape. Its angle of incidence is described by sinθ=R−dR and by n sinθ>sin90^(@)<br>Then(n(R-d))/(R ) gt 1 nR - nd gt R nR -R gt nd R gt (nd)/(n-1)<br>R_(min) =(1.40(100xx10^(-6)m))/(0.40) =350xx 10^(-6)m
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
18 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
18 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
63 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
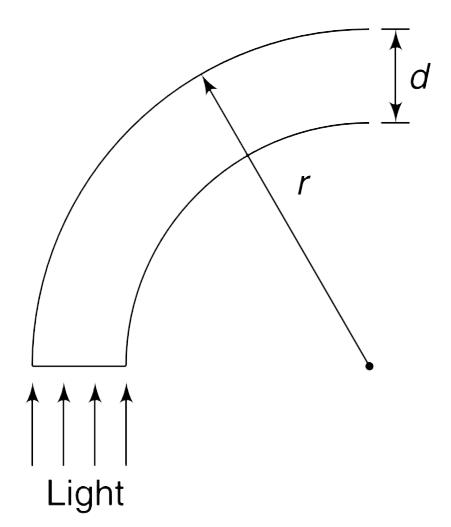
An optical fibre has diameter d and is made of material of refractive indeed μ. It is surrounded by air. Light is made to enter through one end of the fibre as shown. The fiber is in the shape of a circular bend of outer radius r.
(a) Find least value of r(=ro) for which no light can escape out of the fibre. Calculate ro for d=200μm and μ=1.4.
(b) How is value of ro affected as d is made smaller?
(c) For sharper bends, shall we have higher μ or smaller μ ?
View SolutionAn optical fibre of retive index n is surrounded by air. A light ray enters the end of the fibre as shown in the figure. The largest value of ϕ permitted, if the ray incidents on the wall of the fibre at criticál angle for the fibre-air interface, is given by sin(ϕ2)=(xn2−4y)12. Find (xy).
'(##CEN_KSR_PHY_JEE_C26_E01_032_Q14##)'
View Solution
Knowledge Check
A cylinderical optical fibre (quarter circular shape) of refractive index n=2 and diameter d=4mm is surrounded by air. A light beam is sent into the fibre along its axis as shown in figure. Then the smallest outer radius R (as shown in figure) for which no light escapes after incident on curved surface of fibre is:
 .A2mmB4mmC8mmD6mm
.A2mmB4mmC8mmD6mmA ray of light strikes an air-glass interface such that a part of it is reflected into air and the rest enters glass as shown in the figure below.
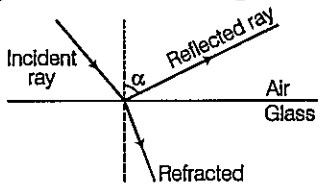
If angle of refraction and refractive index of glass with respect to air is r and μ respectively,then value of α isArBμ sin rCsin−1(μsinr)Dsin−1(sinrμ)What is the least radius through which an optical fiber of core diameter 0.05 mm may be bent (as shown in figure) without serious loss of light? The refractive index of the core is 1.6 and that of cladding is 1.5.
_E01_020_Q01.png) A0.28 mmB0.58 mmC0.78mmD1 mm
A0.28 mmB0.58 mmC0.78mmD1 mm
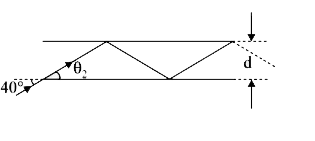
In figure, the optical fiber is l = 2 m long and has a diameter of d=20μm. If a ray of light is incident on one end of the fiber at angle θ1=40∘ , the number of reflections it makes before emerging form the other end is close to : (refractive index of fiber is 1.31 and sin40∘=0.64)
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
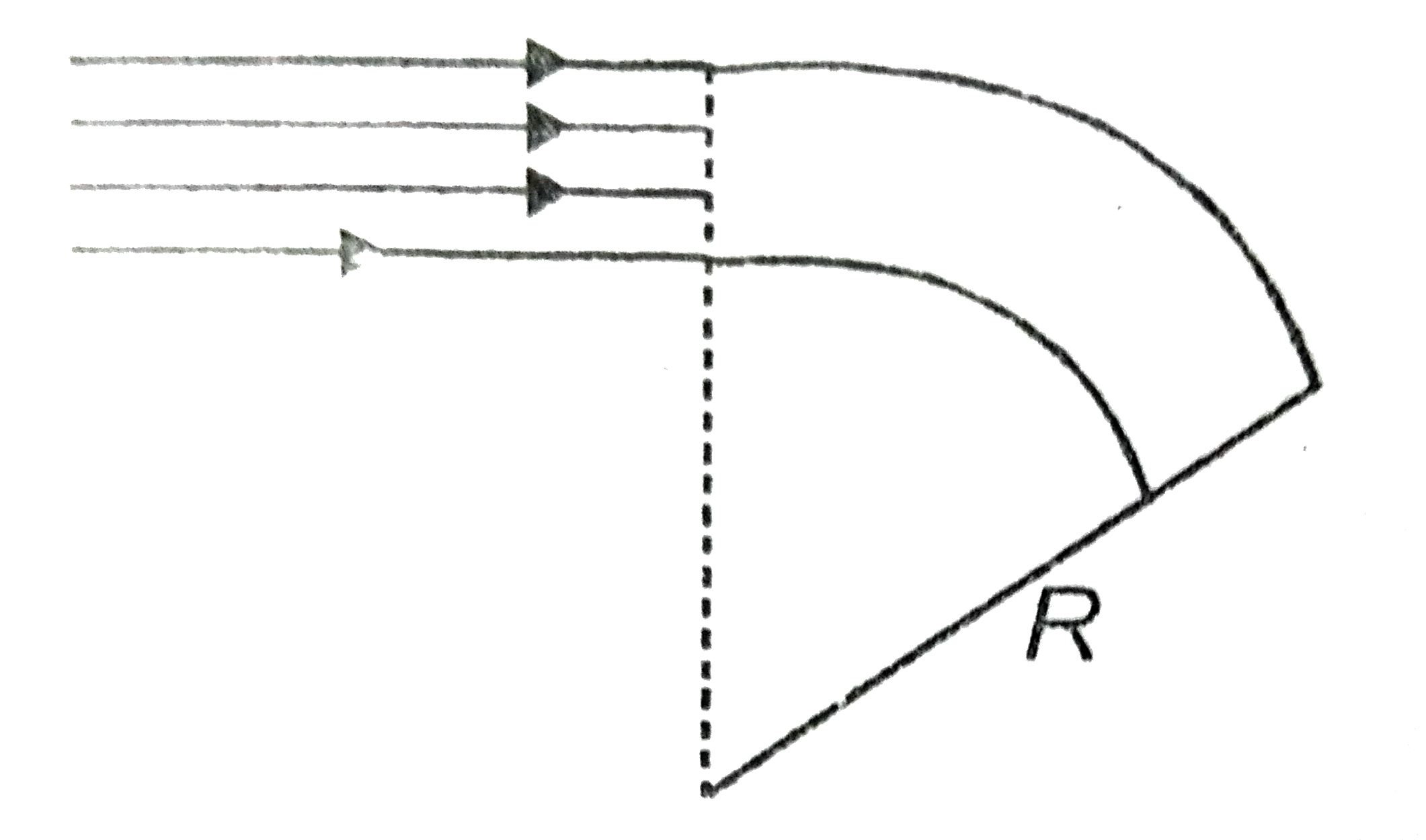
View SolutionA portion of a straight glass rod of diameter 2 cm and refractive index 1.5 is bent into an arc of a circle of radius R cm and a parallel beam of light is incident on it as shown in figure. Find the smallest R which permits all the light to pass around the arc.
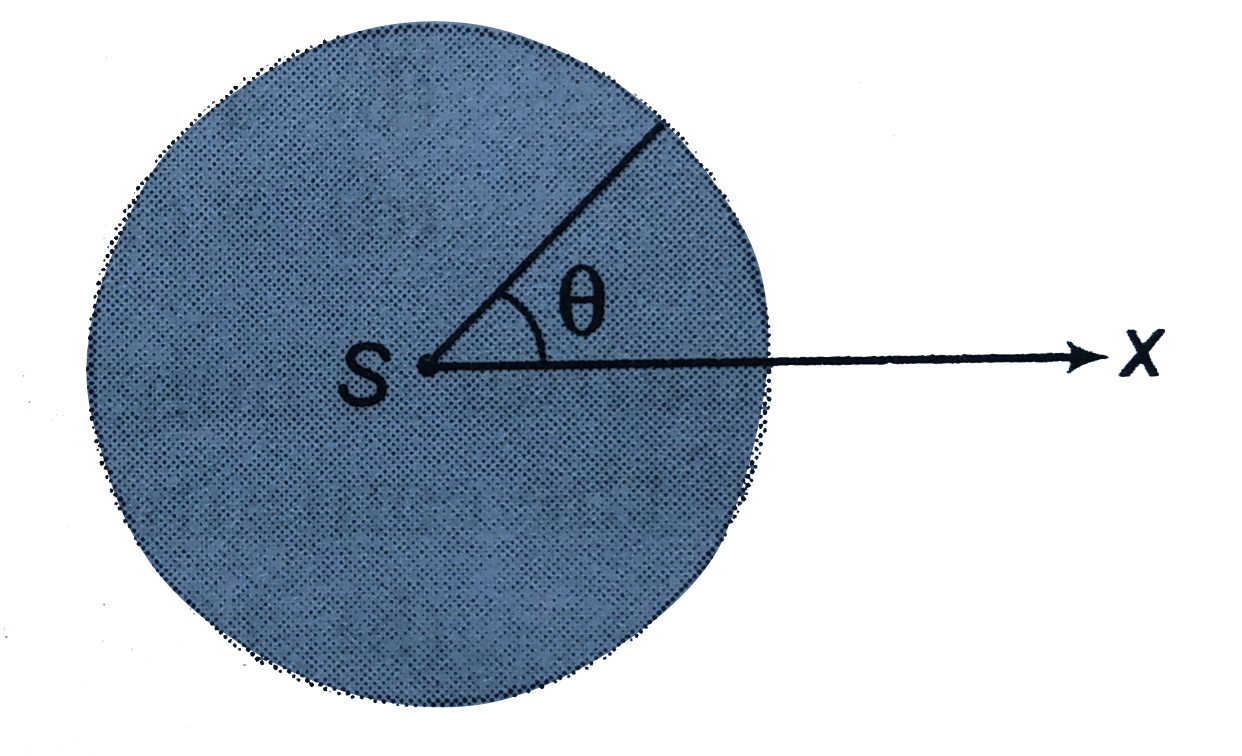
View SolutionA light source S is placed at the centre of a glass sphere of radius R and refractive index μ. The maximum angle θ with the x-axis (as shown in the figure) an incident light ray can make without suffering total internal reflection is
View SolutionA right-angled prism of refractive index μ1, is placed in a rectangular block of refractive index μ2, which is surrounded by a medium of refractive index μ3, as shown in the figure. A ray of light 'e' enters the rectangular block at normal incidence. Depending upon the relationships between μ1,μ2andμ3, it takes one of the four possible paths 'ef','eg','eh'or'ei'.
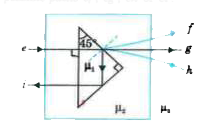
Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists:

View Solution
