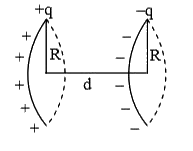
Two current carrying coil having radius 'r' are seperated by distance 'd' as shown in diagram. If r<<d. Then find the force between two ring. Current in both the ring is clockwise and equal to i.
6μ04πi2π2r4d4
μ04πi2π2r4d4
3μ04πi2π2r4d4
μ02πi2π2r4d4
The correct Answer is:A
f=μdBdx
B=2μ0M4πd3⇒dBdd=−6μ0M4πd4
F=M1M2[−6μ04πd4]=−64πμ0M1M2d4
−6μ0(πr2i)(π2i)4πd4
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
18 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
18 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
63 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
Knowledge Check
There will be no force between two current carrying wires if currents are
Aparallel to each otherBantiparallel to each otherCperpendicular to each otherDnothing can be saidTwo thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are +Q and −Q. The potential difference between the centre so the two rings is
AzeroBQ4πε0[1R−1√R2+d2]CQ4πε0d2)DQ2πε0[1R−1√R2+d2]Two thin wire rings each having a radius R are placed at a distance d apart with their axes coiciding. The charges on the two rings are +q and −q. The potential difference between the centres of the two rings is
A(a) q2π∈0[1R−1√R2−d2]B(b) qR4π∈0d2C(c) q4π∈0[1R−1√R2+d2]D(d) zero
Two thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are +Q and −Q. The potential difference between the centre so the two rings is
View SolutionTwo long straight parallel conductors of length l ,separated by a distance d and each carrying a current I attract each other with a force equal to
View SolutionA strong magnet is placed under a horizontal conducting ring of radius r that carries current i as shown in Fig. If the magnetic field makes an angle θ with the vertical at the ring's location, what are the magnitude and direction of the resultant force on the ring?
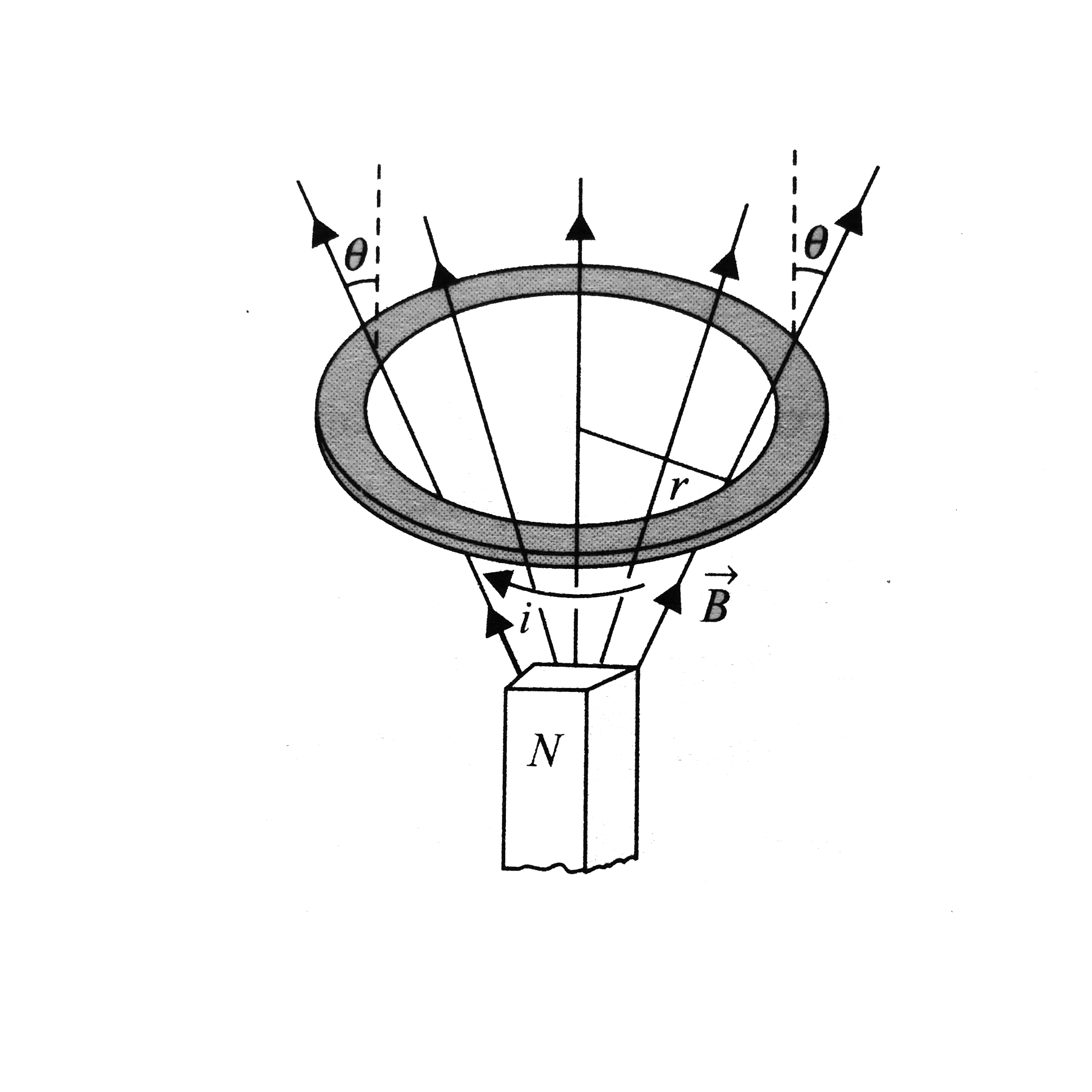
View SolutionA strong magnet is placed under a horizontal conducting ring of radius r that carries current i as shown in Fig. If the magnetic field makes an angle θ with the vertical at the ring's location, what are the magnitude and direction of the resultant force on the ring?

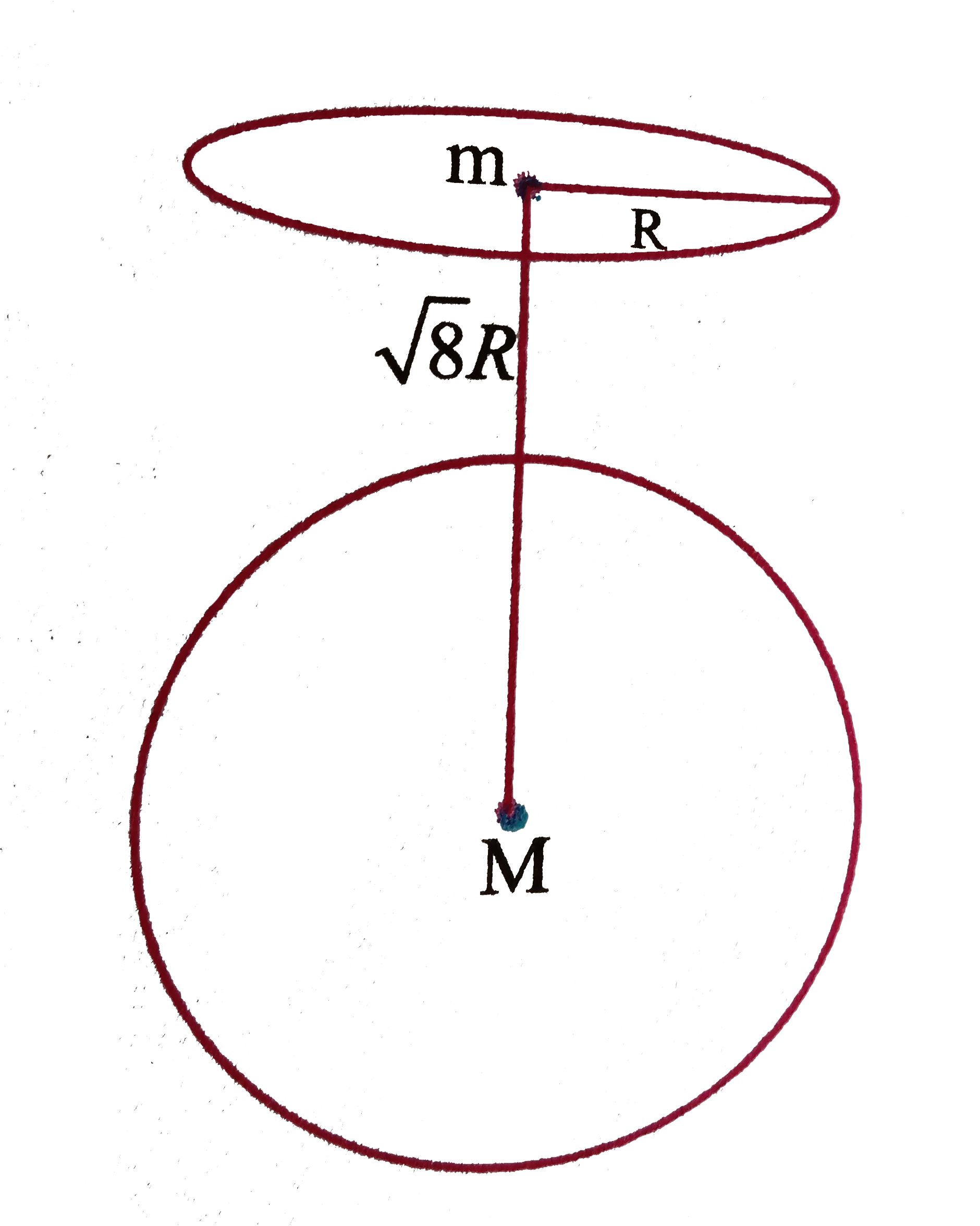
View SolutionThe centres of a ring of mass m and a sphere of mass M of equal radius R, are at a distance √8R apart as shown. The force of attraction between the ring and the sphere is
View Solution