A long piece of paper is being pulled on a horizontal surface with a c

Topper's Solved these Questions

BOOK - ARIHANTCHAPTER - MOMENTUM AND CENTRE OF MASSEXERCISE - Momentum And Center of Mass
117videos
MOMENTUM AND CENTRE OF MASS
BOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS
159videos
ROTATIONAL MOTION

Knowledge Check

Question 1 - Select One
A block is resting on a horizontal plate in the xy plane and the coefficient of friction between block and plate is $μ$ . The plate begins to move with velocity $v = b t^{2}$ in x direction At what time will the block start sliding on the plate?
A $\frac{μ b}{g}$
B $\frac{μ b g}{2}$
C $\frac{μ g}{b}$
D $\frac{μ g}{2 b}$
Question 2 - Select One or More
A long block A is at rest on a smooth horizontal surface. A small block B, whose mass is half of A, is placed on A at one end and projected along A with some velocity u. The coefficient of friction between the blocks is $μ$ :

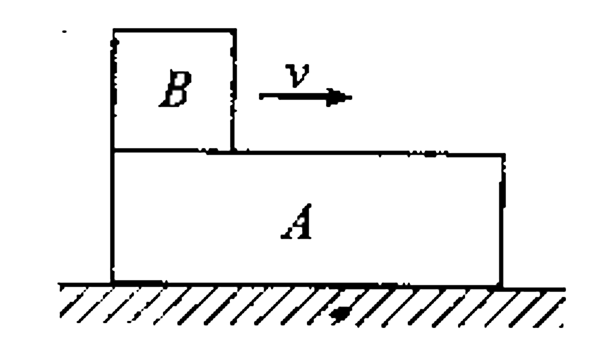AThe blocks will reach the final common velocity $\frac{u}{3}$
Bthe work done against friction is two-thirds of the initial kinetic energy of B
Cbefore the block reach a common velocity the acceleration of A relative to B is $\frac{2}{3} μ g .$
DBefore the blocks reach a common velocity the acceleration of A relative to B is $\frac{3}{2} μ g .$
Question 3 - Select One
A block of mass $m$ is moving with a speed $v$ on a horizontal rough surface and collides with a horizontal mounted spring of spring constant $k$ as shown in the figure .The coefficient of friction between the block and the floor is $μ$ The maximum compression of the spring is

A $- \frac{μ m g}{k} + \frac{1}{k} \sqrt{{(μ m g)}^{2} + m k v^{2}}$
B $\frac{μ m g}{k} + \frac{1}{k} \sqrt{{(μ m g)}^{2} + m k v^{2}}$
C $- \frac{μ m g}{k} + \frac{1}{k} \sqrt{{(μ m g)}^{2} - m k v^{2}}$
D $\frac{μ m g}{k} + \frac{1}{k} \sqrt{{(μ m g)}^{2} + m k v^{2}}$

The correct Answer is: $V_{max} = \frac{- u^{2}}{2} + (\frac{u^{4}}{4} + {(2 μ g l)}^{2})$

Topper's Solved these Questions

Similar Questions

Knowledge Check

A block is resting on a horizontal plate in the xy plane and the coefficient of friction between block and plate is $μ$ . The plate begins to move with velocity $v = b t^{2}$ in x direction At what time will the block start sliding on the plate?

A long block A is at rest on a smooth horizontal surface. A small block B, whose mass is half of A, is placed on A at one end and projected along A with some velocity u. The coefficient of friction between the blocks is $μ$ :

A block of mass $m$ is moving with a speed $v$ on a horizontal rough surface and collides with a horizontal mounted spring of spring constant $k$ as shown in the figure .The coefficient of friction between the block and the floor is $μ$ The maximum compression of the spring is

ARIHANT-NEWTONS LAWS OF MOTION-All Questions

The correct Answer is:Vmax=−u22+(u44+(2μgl)2)

Topper's Solved these Questions

Similar Questions

Knowledge Check

A block is resting on a horizontal plate in the xy plane and the coefficient of friction between block and plate is μ. The plate begins to move with velocity v=bt2 in x direction At what time will the block start sliding on the plate?

A long block A is at rest on a smooth horizontal surface. A small block B, whose mass is half of A, is placed on A at one end and projected along A with some velocity u. The coefficient of friction between the blocks is μ:

A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is

ARIHANT-NEWTONS LAWS OF MOTION-All Questions

The correct Answer is: $V_{max} = \frac{- u^{2}}{2} + (\frac{u^{4}}{4} + {(2 μ g l)}^{2})$

A block is resting on a horizontal plate in the xy plane and the coefficient of friction between block and plate is $μ$ . The plate begins to move with velocity $v = b t^{2}$ in x direction At what time will the block start sliding on the plate?

A long block A is at rest on a smooth horizontal surface. A small block B, whose mass is half of A, is placed on A at one end and projected along A with some velocity u. The coefficient of friction between the blocks is $μ$ :

A block of mass $m$ is moving with a speed $v$ on a horizontal rough surface and collides with a horizontal mounted spring of spring constant $k$ as shown in the figure .The coefficient of friction between the block and the floor is $μ$ The maximum compression of the spring is