A massless spring of force constant K and natural length l0 is hanging from a ceiling. An insect of mass m is sitting at the lower end of the spring and the system is in equilibrium . The insect starts slowing climbing up the spring so as to eat a bug sitting on the ceiling. Assume that insect climbs without slipping on the spring and K=mgl0 . find the length of the spring when the insect is at 14th of its original distance from the bug .
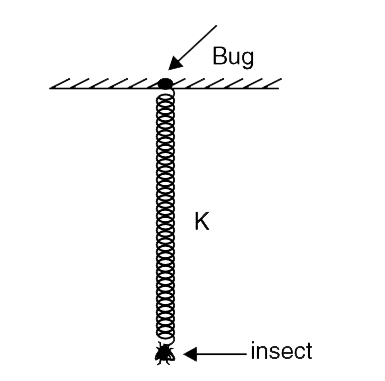
The correct Answer is:5l04
Step by step video, text & image solution for A massless spring of force constant K and natural length l_(0) is hanging from a ceiling. An insect of mass m is sitting at the lower end of the spring and the system is in equilibrium . The insect starts slowing climbing up the spring so as to eat a bug sitting on the ceiling. Assume that insect climbs without slipping on the spring and K = (mg)/(l_(0)) . find the length of the spring when the insect is at (1)/(4)th of its original distance from the bug . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Springs of apring constants k,2k,4k,8k . . . Are connected in series. A mass m kg is attached to the lower end of the last spring and the system is allowed to vibrate. What is the time period of oscillations?
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View Solution
Knowledge Check
A particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
Amω2l0kBmω2l0k−mω2Ckl0k−mω2Dmω2l0k+mω2A massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is
Ag√mkBg√2mkCg2√mkDg√m2kAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
A(a) 4MgkB(b) 2MgkC(c) MgkD(d) Mg2k
A massless spring with a force constant K=40N/m hangs vertically from the ceiling.A 0.2kg block is attached to the end of the spring and held in such a position that the spring has its natural length and suddenyl released. The maximum elastic strain energy stored in the spring is (g=10m/s2)
View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
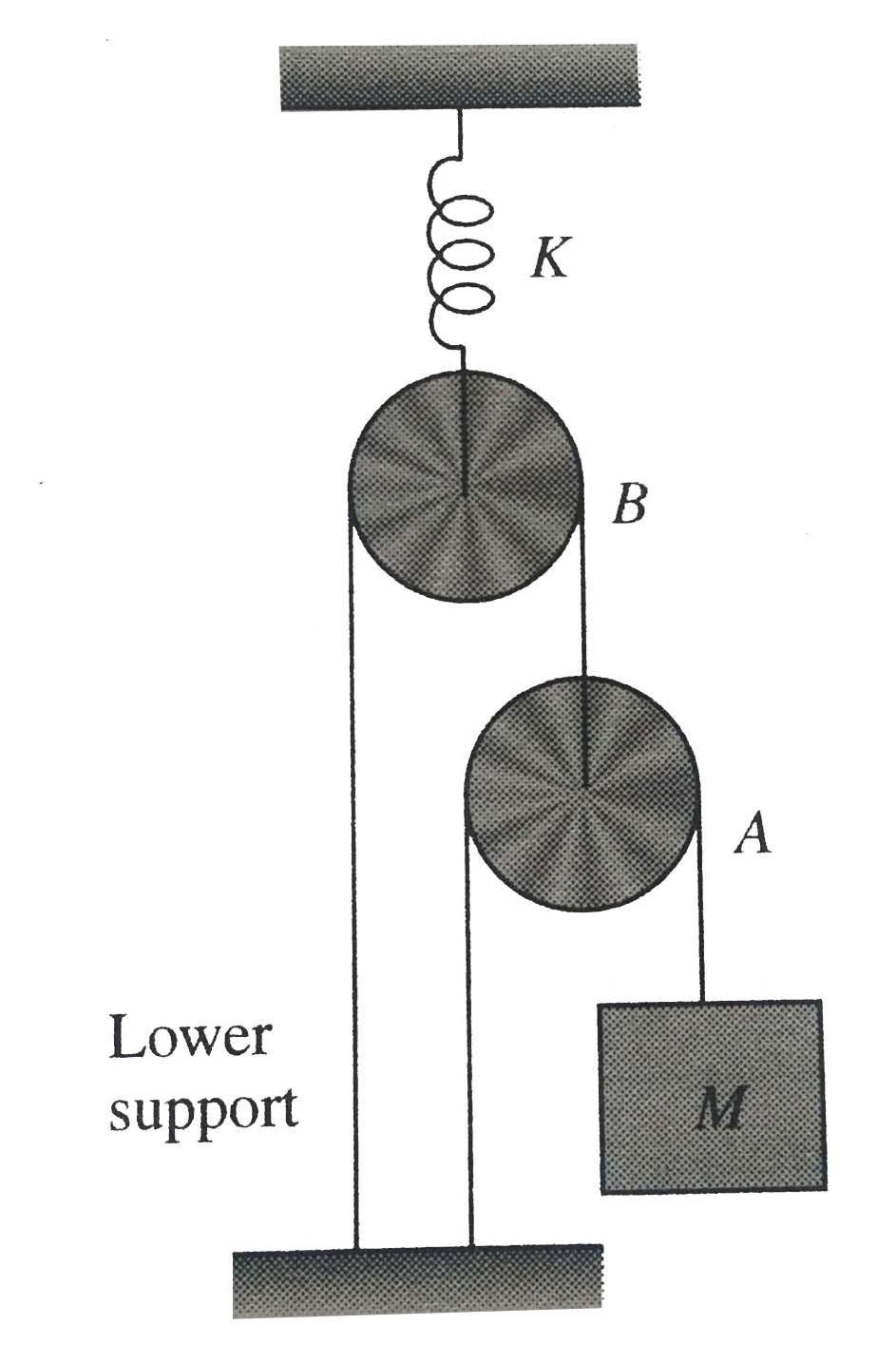
The extension produced in the spring is given by
View SolutionAn ideal spring with spring - constant K is bung from the colling and a block of mass M is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
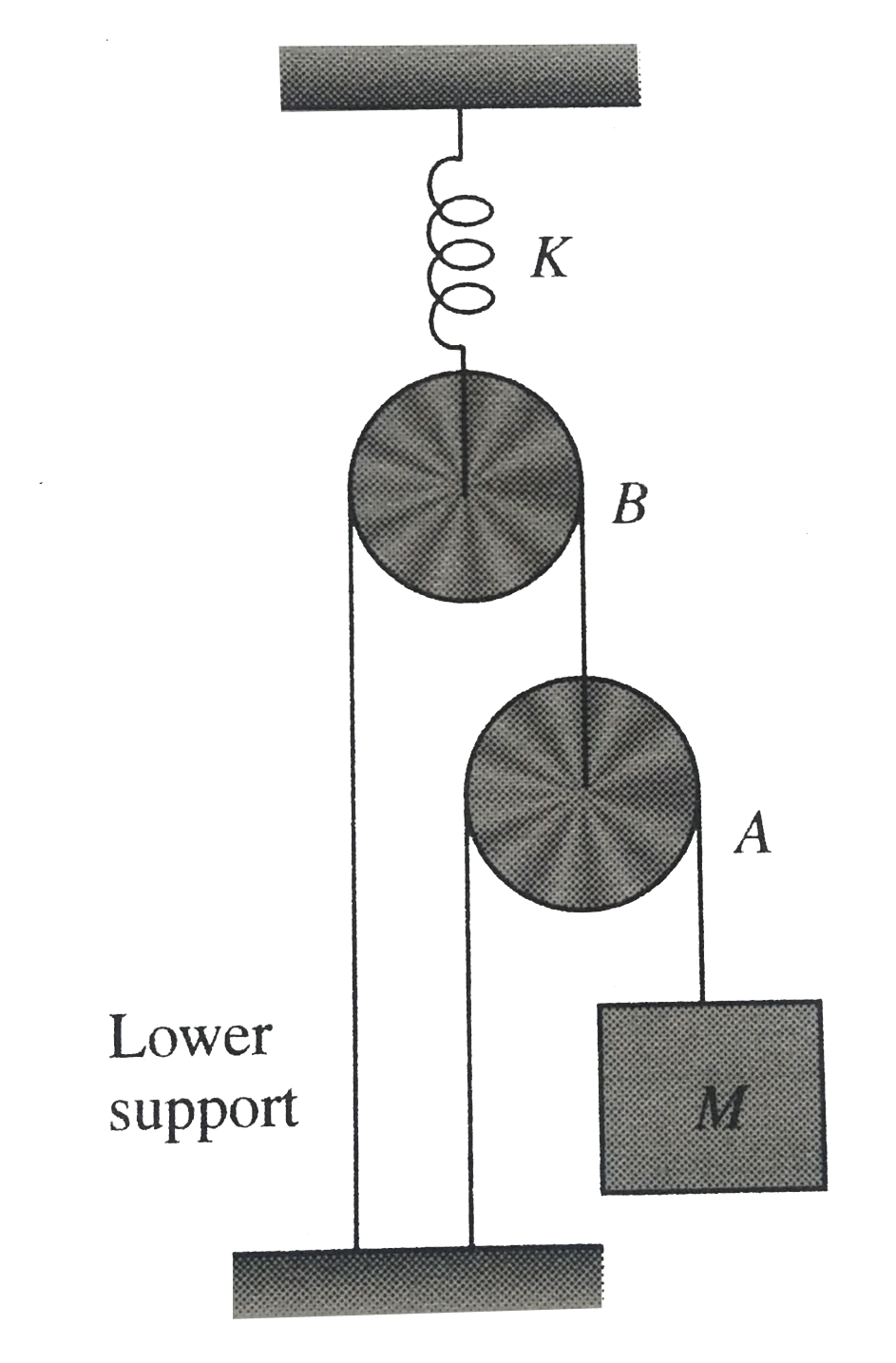
Find the net tension force acting on the lower support.
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is

View Solution
