A car is being driven on a tilted ground. The ground makes an angle θ with the horizontal. The driven drives on a circle of radius R. The coefficient of friction between the tires and the ground is μ.
(a) What is the largest speed for which the car will not slip at point A? Assume that rate of change of speed is zero.
(b) What is the largest constant speed with which the car can be driven on the circle without slipping?
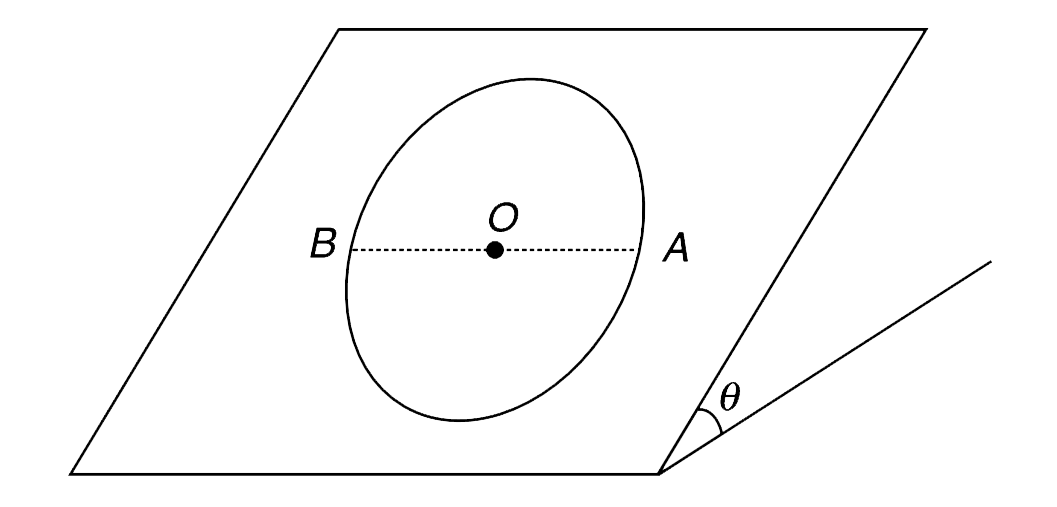
The correct Answer is:(a) [g2R2(μ2cos2θ−sin2θ)]1/4
√gR(μcosθ−sinθ)
Topper's Solved these Questions
Similar Questions
Knowledge Check
A particle is fired from a point on the ground with speed u making an angle θ with the horizontal.Then
Athe radius of curvature of the projectile at the highest point is u2cos2θgBthe radius of curvature of the projectile at the highest point is u2sin2θgCat the point of projection magnitude of tangential acceleration is gsinθDat the point of projection magnitude of tangential acceleration is gcosθA car is travelling along a curved road of radius r. If the coefficient of friction between the tyres and the road is μ the car will skid if its speed exceeds .
A2√μrgB√3μrgC√2μrgD√μrgA car is taking turn on a circular path of radius R. If the coefficient of friction between the tyres and road is μ, the maximum velocity for no slipping is
AμRgB2μRgC(μRg)1/2D(2μRg)1/2
A car is taking turn on a circular path of radius R. If the coefficient of friction between the tyres and road is μ, the maximum velocity for no slipping is
View SolutionA car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tire and the road is μs=2.0, find the maximum speed the car can take without skidding.
View SolutionA cyclist speeding at 6ms−1 in a circle of 18 m radius makes an angle θwith the vertical. Calculate θ. Also determine the minimum possible value of the coefficient of friction between the tyres and the ground?
View SolutionA cyclist speeding at 6ms−1 in a circle of 18 m radius makes an angle θwith the vertical. Calculate θ. Also determine the minimum possible value of the coefficient of friction between the tyres and the ground?
View SolutionThe maximum speed of a car which can be safely driven along a curve of radius 10 m , If the coefficient of friction between the tyres and the road is 0.5, is (g=9.8m/s2)
View Solution
