A water tank has a circular hole at its base. A solid cone is used to plug the hole. Exactly half the height of the cone protrudes out of the hole. Water is filled in the tank to a height equal to height of the cone. Caluclate the buoyancy force on the conc. Density of water is ρ and volume of cone is V.
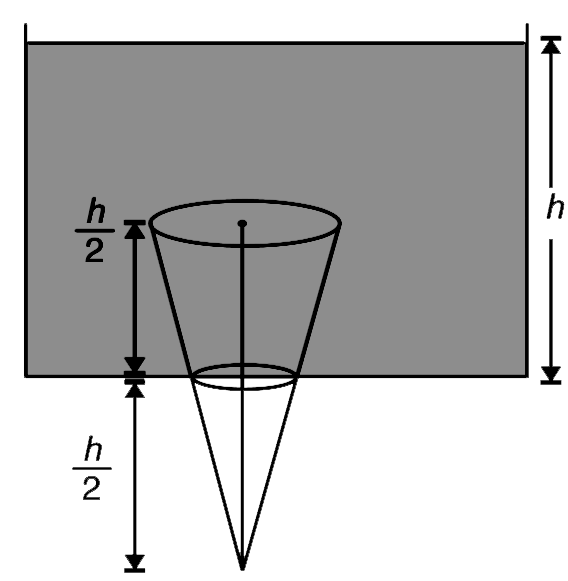
A water tank has a circular hole at its base. A solid cone is used to plug the hole. Exactly half the height of the cone protrudes out of the hole. Water is filled in the tank to a height equal to height of the cone. Caluclate the buoyancy force on the conc. Density of water is rho and volume of cone is V.

Text Solution
Verified by Experts

The correct Answer is:Vρg/8

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 11PHYSICSFLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The radius of the base and the height of a right circular cone are doubled. The volume of the cone will be

    A8 times of the previous volume
    Bthree times of the previous volume
    C3√2 times of the previous volume
    D6 times of the previous volume

  • The height of a cone is equal to the radius of its base. The radius of a sphere is equal to the radius of the base of the cone. The ratio of the volume of the cone to the volume of the sphere is

    A112
    B14
    C13
    D11

  • A large tank having a small hole at the bottom is filled with water to a height h. If the stream of water coming out of the hole is directed vertically upwards it will :

    Arise to height h
    Brise to a heighet less than h
    Crise to a height greater than h
    Dnot rise at all