Two soap bubbles of radius R1andR2(<R1) are joined by a straw. Air flows from one bubble to another and a single bubble of radius R3 remains.
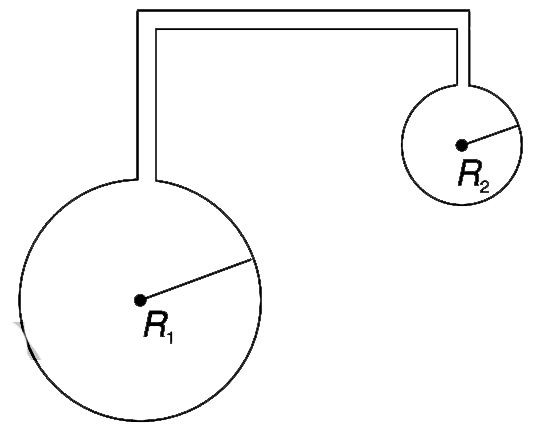
(a) From which bubble does the air flow out ?
(b) Assuming no temperature change and atmospheric pressure to be P_(o), find the surface tension of the soap solution.
The correct Answer is:(a) From smaller bubble (b) T=(PoR33−R31−R324(R21+R22−R23)
Step by step video, text & image solution for Two soap bubbles of radius R_(1) and R_(2) (lt R_(1)) are joined by a straw. Air flows from one bubble to another and a single bubble of radius R_(3) remains. (a) From which bubble does the air flow out ? (b) Assuming no temperature change and atmospheric pressure to be P_(o), find the surface tension of the soap solution. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Two soap bubbles of radii R1andR2 kept in atmosphere are combined isothermally to form a big bubble of radius R. The expression for surface tension will be
AP0(R3+R31+R32)4(R2+R21+R22)BP0(R31+R32−R3)4(R2−R21−R22)CP0(R31+R32−R3)D4P0(R31+R32−R3) - Question 2 - Select One
Prove that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
Ar2−r1Br2−r1r1r2Cr1r2r2−r1Dr2+r1
Find the work done in blowing a soap bubble of radius R if pressure outside in p0 and the surface tension of the soap solution is T.
View SolutionTwo soap bubbles of radius r1 and r2 combine. Find radius of curvature of the common surface separating them.
 View Solution
View SolutionTwo soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
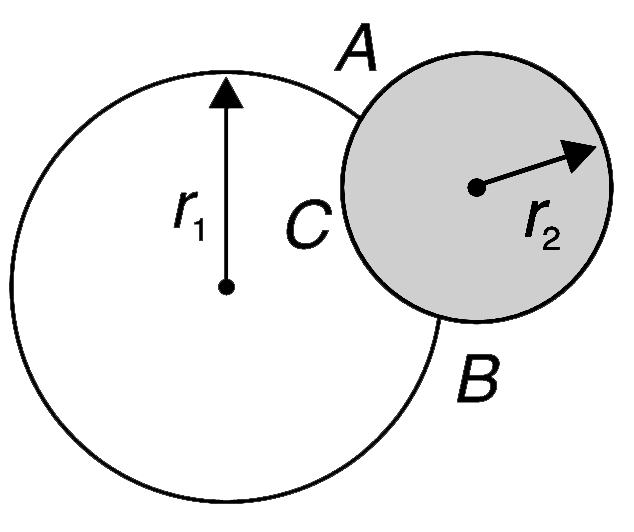 View Solution
View SolutionTwo soap bubble of radii R1 and R2 are kept in vacuum at constant temperature, the ratio of masses of air inside them, is
View SolutionWhat is the excess of pressure inside a soap bubble of radius 3cm if the surface tension of the soap solution is 30 dyn/cm ?
View SolutionA soap bubble of radius R has formed at normal temperature and pressure under isothermal conditions. Complete the work done. The surface tension of soap solution is T.
View Solution

