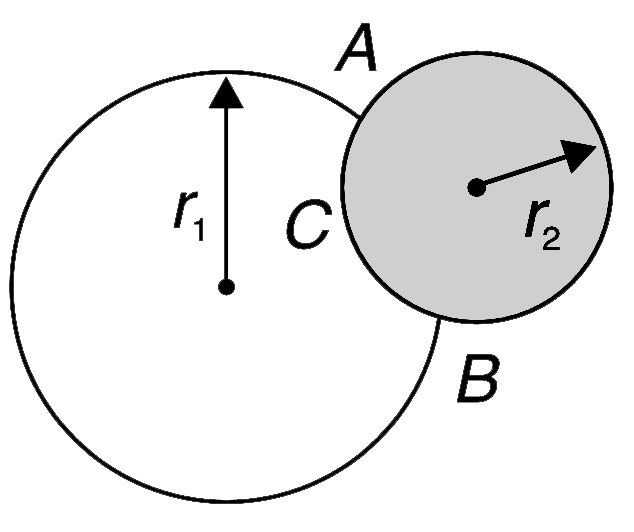
(a) In the last question find the angle between the tangents drawn to the bubble surfaces at point A.
(b) In the above question assume that r1=r2=r. What is the shape of the common interface ACB? Find length AB in this case.
(c) With r1=r2=r the common wall bursts and the two bubbles form a single bubble find the radius of this new bubble. It is given that volume of a truncated sphere of radius R and height y is π3y2(3R−y) [see figure]
![(a) In the last question find the angle between the tangents drawn to the bubble surfaces at point A. (b) In the above question assume that r(1) = r(2) = r. What is the shape of the common interface ACB? Find length AB in this case. (c) With r(1) = r(2) = r the common wall bursts and the two bubbles form a single bubble find the radius of this new bubble. It is given that volume of a truncated sphere of radius R and height y is pi/3 y ^(2) (3R -y) [see figure]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C09_E01_021_Q01.png)
The correct Answer is:(a)120∘ (b) √3r (c) 3r2(2)1/3
Step by step video, text & image solution for (a) In the last question find the angle between the tangents drawn to the bubble surfaces at point A. (b) In the above question assume that r_(1) = r_(2) = r. What is the shape of the common interface ACB? Find length AB in this case. (c) With r_(1) = r_(2) = r the common wall bursts and the two bubbles form a single bubble find the radius of this new bubble. It is given that volume of a truncated sphere of radius R and height y is pi/3 y ^(2) (3R -y) [see figure] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the common radius of curvature when two soap bubbles with radii r1
Ar=r1+r22Br=r1+r2r1−r2Cr=r1r2r1+r2Dr=√r1r2 - Question 2 - Select One
The radii of two soap bubbles are ri and r2. In isothermal conditions, two meet together in vacuum. Then the radius kof the resultant bubble is given by
AR=(r1+r2)/2BR=r1(r1r2+r2)CR2=r21+r22DR=r1+r2 - Question 3 - Select One
Prove that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
Ar2−r1Br2−r1r1r2Cr1r2r2−r1Dr2+r1
Two soap bubbles are stuck together with an intermediate film separating them. Compute the radius of curvature of this film given that the radii of the bubbles in this arrangement are r1 and r2 respectively. If r1>r2 state clearly which way the intermediate film will bulge.
For the case when r1=r2=2cm calculate he radius of the bubble formed by bursting the intermediate film. The volume of a spherical dome of radius R and height h is πb2(3R−b)/3.View SolutionIn ΔABC, if r1<r2<r3, then find the order of lengths of the sides
View SolutionTwo soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
 View Solution
View SolutionTwo circles of radius r1andr2 touches externally at point A have a common tangent PQ. Then find the value of PQ2.
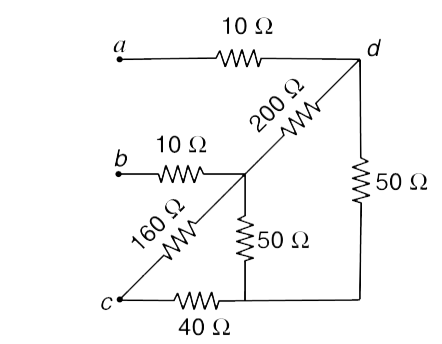
View SolutionIn the circuit shown in the fig the equivalent resistance between aandb is Rab and the equivalent between aandc is Rac. find the ratio Rab:Rac.
 View Solution
View Solution


