An insulated cylindrical vessel is divided into three identical parts by two partitions 1 and 2. The left part contains O2 gas, the middle part has N2 and the third chamber has vacuum. The average molecular speed in oxygen chamber is V0 and that in nitrogen chamber is √87V0. Pressure of the gases in two chambers is same. Partition 1 is removed and the gases are allowed to mix. Now the stopper holding the partition 2 is removed and it slides to the right wall of the container, so that the mixture of gases occupy the entire volume of the container.
Find the average speed of O2 molecules now.
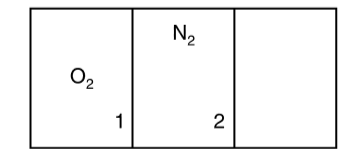
The correct Answer is:V0
Step by step video, text & image solution for An insulated cylindrical vessel is divided into three identical parts by two partitions 1 and 2. The left part contains O_(2) gas, the middle part has N_(2) and the third chamber has vacuum. The average molecular speed in oxygen chamber is V_(0) and that in nitrogen chamber is sqrt((8)/(7)) V_(0). Pressure of the gases in two chambers is same. Partition 1 is removed and the gases are allowed to mix. Now the stopper holding the partition 2 is removed and it slides to the right wall of the container, so that the mixture of gases occupy the entire volume of the container. Find the average speed of O_(2) molecules now. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ARIHANTCHAPTER - KINETIC THEORY OF GASESEXERCISE - Level 218videos
KINETIC THEORY OF GASES
- BOOK - ARIHANTCHAPTER - KINETIC THEORY OF GASESEXERCISE - Level 34videos
KINETIC THEORY OF GASES
- BOOK - ARIHANTCHAPTER - KINEMATICSEXERCISE - Level 333videos
KINEMATICS
- BOOK - ARIHANTCHAPTER - MOMENTUM AND CENTRE OF MASSEXERCISE - Momentum And Center of Mass117videos
MOMENTUM AND CENTRE OF MASS
Similar Questions
The rms speed of molecules of an ideal gas is vrms. Obtain the expression for rms value of relative speed for all pair of molecules in a gas sample.
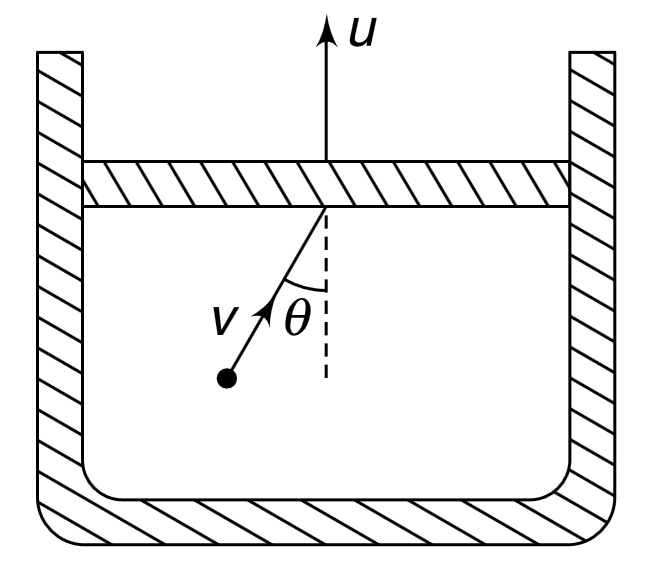
02:21View SolutionAn ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy
 04:41View Solution
04:41View SolutionA car manufacturer usually tells a optimum speed (V0) at which the car should be driven to get maximum mileage. In order to find the optimum speed for a new model, an engineer of the car company experimented a lot and finally plotted a graph between the extreme time t (defined as number of hours a tank full of petrol lasts) vs the constant speed V at which car was run.
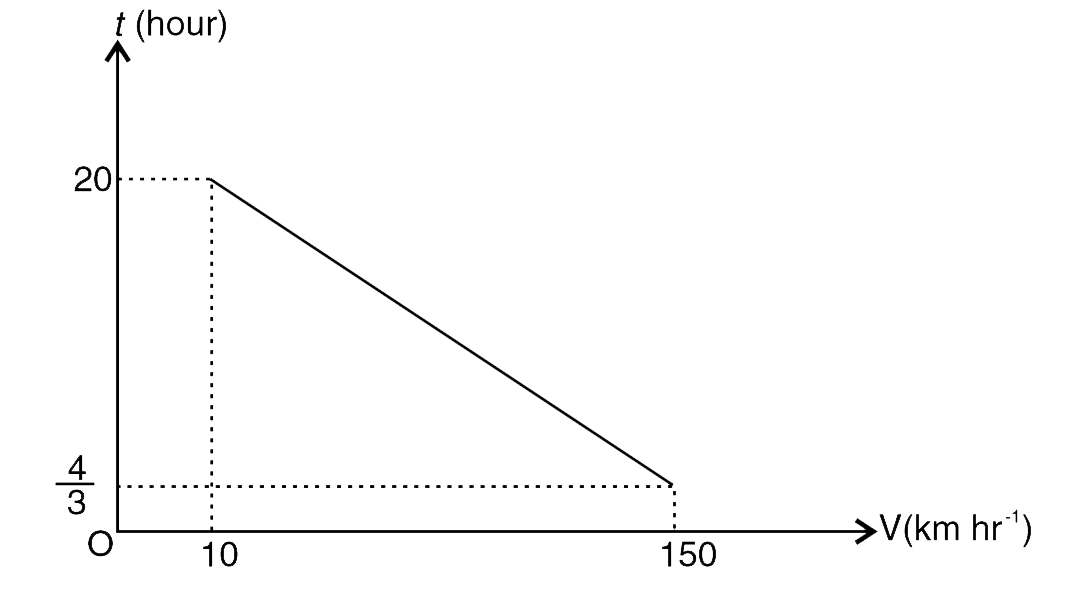
(a) Calculate the optimum speed V0 for this new model.
(b) If the fuel tank capacity of this car is 50 litre, what maximum mileage can be obtained from this car?04:06View SolutionA particle is acted upon by a force for 1 second whose X component remains constant at Fx=30N but y and z components vary with time as shown in the graph. Calculate the magnitude of change in momentum of the particle in 1 s. What angle does the change in momentum (Δ→P) make with X axis ?
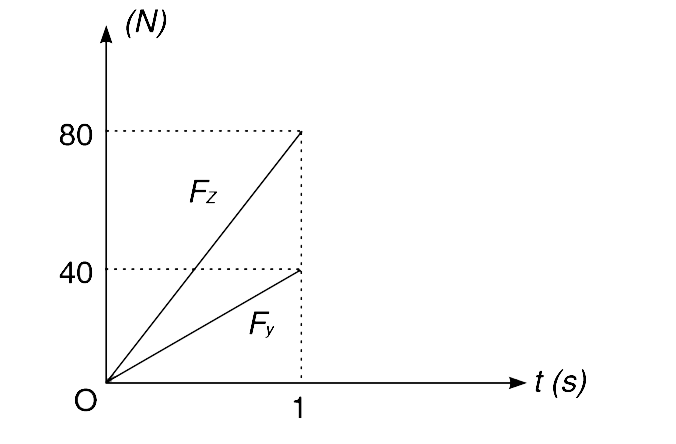 03:10View Solution
03:10View SolutionThe container shown in Fig. 9(EP).6 has two chambers, separated by a partition, of volumes V_(1) = 2.0 litre and V_(2) = 3.0 litre . The chambers contains mu_(1) = 4.0 and mu_(2) = 5.0 "moles" of a gas at pressures p_(1) = 1.00 atm and p_(2) = 2.00 atm . calculate the pressure after the partition is removed and the mixture attains equilibrium.
10:05View SolutionA vessel is divided by a solid partition into two parts of equal volume. One part is filled with nitrogen and the other with carbon monoxide. It may be assumed that the cross-sect.ional areas of the molecules of the two gases are the same. The relative molecular masses of hoth gases are also the same (equal to 28). Finally, the pressures in both parts are the same. After the partition is lifted, the gases begin to diffuse into each other. flow does the amount of each gas that has transferred to the part occupied by the other gas depend on the initial pressures of the gases?
View SolutionConsider the adjacent figure. A piston divides a cylindrical container into two equal parts. The lets part contains 1 mole of helium gas and the right part contains two moles or oxygen gas. The initial temperatures and pressures of the gases in the left chamber are T_(0) and p_(0) and the right chamber are (T_(0))/(2) and p_(0) respectively as shown in the figure. The piston as well as the walls of the container are adiabatic. After removal of the piston, gases mix homoganeously and the final pressure becomes p=(4n)/(13)p_(0) . Find the value of n.
02:31View SolutionThe container shown in figure has two chambers separated by a partition of volumes V_(1) =2.0 L and V_(2) =3.0 L . The chambers contain mu_(1) 4.0 and mu_(2)=5.0 mole of a gas at pressure p_(1) =1.00 atm and P_(2) =2.00 atm. Calculate the pressure after the partition is removed and the mixture attains equilibrium.
06:12View SolutionA rectangualr box (shown in figure) has a movable and smooth portition which can slide along the length of the box. Both chambers contains 1 mole of monoatomic gas (γ=53) at a pressure walls of box and partition are thermally insulated. Due to heating, gas in left chamber expands until pressure in both chambers become 32P0 determine
(a) The final temperature of gas in each chamber
(b) The work done by the gas in the right chamber.
 05:22View Solution
05:22View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V_(1) and contains ideal gas at pressure P_(1) and temperature T_(1) . The other chambers has volume V_(2) and contains ideal gas at pressure P_(2) and temperature T_(2) . If the partion is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
06:16View SolutionOne mole of PCl5 is heated in one litre closed container. If 0.6 mole of chlorine is found at equilibrium, calculate the value of equilibrium constant.
05:51View SolutionThe container shown in figure has two chambers separated by a partition of volumes V_(1) =2.0 L and V_(2) =3.0 L . The chambers contain mu_(1) 4.0 and mu_(2)=5.0 mole of a gas at pressure p_(1) =1.00 atm and P_(2) =2.00 atm. Calculate the pressure after the partition is removed and the mixture attains equilibrium.
04:25View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V_1 and contains ideal gas at pressure P_1 and temperature T_1 .The other chamber has volume V_2 and contains ideal gas at pressure P_2 and temperature T_2 . If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
04:06View SolutionA container is divided into two chambers by a partition. The volume of first chamber is 4.5 litre and second chamber is 5.5 litre. The first chamber contain 3.0 moles of gas at pressure 2.0 atm and second chamber contain 4.0 moles of gas at pressure 3.0 atm. After the partition is removed and the mixture attains equilibrium, then, the common equilibrium pressure existing in the mixture is "x"xx10^(-1) atm. Value of x is "___" .
05:45View SolutionConsider the adjacent figure. A piston divides a cylindrical container into two equal parts. The lets part contains 1 mole of helium gas and the right part contains two moles or oxygen gas. The initial temperatures and pressures of the gases in the left chamber are T_(0) and p_(0) and the right chamber are (T_(0))/(2) and p_(0) respectively as shown in the figure. The piston as well as the walls of the container are adiabatic. After removal of the piston, gases mix homoganeously and the final pressure becomes p=(4n)/(13)p_(0) . Find the value of n.
View Solution

