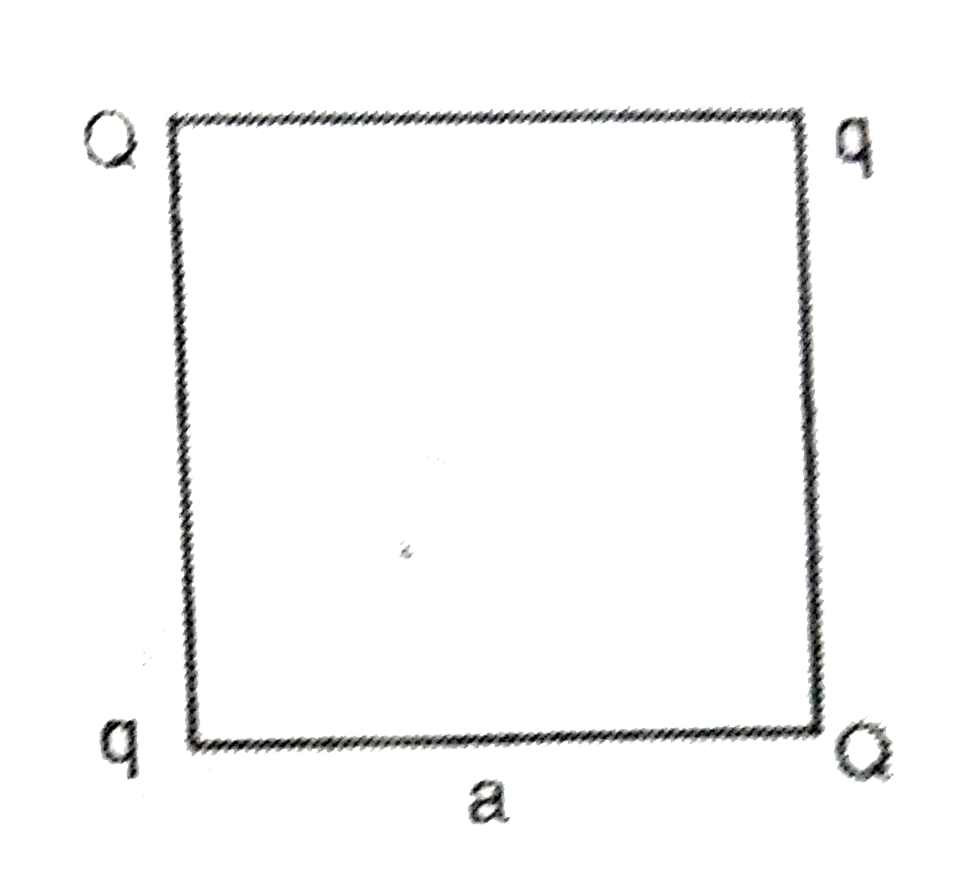
For the system in figure find Q for which resultant force on q is zero.
To solve the problem of finding the value of Q for which the resultant force on the small charge q is zero, we can follow these steps:
Step 1: Understand the Forces Acting on q
We have two small charges q and a charge Q. The forces acting on q are:
- The repulsive force from the other small charge q.
- The attractive force from the charge Q.
Since both small charges q have the same sign, they will repel each other. Therefore, we need to find the value of Q such that the attractive force from Q balances the repulsive force from the other q.
Step 2: Calculate the Repulsive Force FR
The repulsive force FR between the two small charges q is given by Coulomb's law:
FR=k⋅q2r2
where k is Coulomb's constant and r is the distance between the two charges. In this case, if the distance between the charges is the diagonal of a square with side length A, then:
r=√2A
Thus, the repulsive force becomes:
FR=k⋅q2(√2A)2=k⋅q22A2
Step 3: Calculate the Attractive Force FA from Charge Q
The attractive force FA between the charge Q and the small charge q is also given by Coulomb's law:
FA=k⋅|Q|⋅qA2
Here, A is the distance between Q and q.
Step 4: Set the Forces Equal for Equilibrium
For the resultant force on q to be zero, the attractive force FA must equal the repulsive force FR:
FA=FR
Substituting the expressions for FA and FR:
k⋅|Q|⋅qA2=k⋅q22A2
Step 5: Simplify the Equation
We can cancel k and A2 from both sides (assuming k and A are non-zero):
|Q|⋅q=q22
Step 6: Solve for Q
Dividing both sides by q (assuming q≠0):
|Q|=q2
Step 7: Determine the Sign of Q
Since the force between the two small charges q is repulsive, Q must have an opposite sign to q to provide the necessary attractive force. Therefore:
- If q is positive, Q must be negative.
- If q is negative, Q must be positive.
Thus, we can conclude:
Q = -\frac{q}{2} \quad \text{(if q > 0 )}
or
Q = \frac{|q|}{2} \quad \text{(if q < 0 )}
Summary
The value of Q for which the resultant force on q is zero is:
Q = -\frac{q}{2} \quad \text{(if q > 0 )} \quad \text{or} \quad Q = \frac{|q|}{2} \quad \text{(if q < 0 )}
---
We have two small charges q and a charge Q. The forces acting on q are:
- The repulsive force from the other small charge q.
- The attractive force from the charge Q.
The repulsive force FR between the two small charges q is given by Coulomb's law:
FR=k⋅q2r2
where k is Coulomb's constant and r is the distance between the two charges. In this case, if the distance between the charges is the diagonal of a square with side length A, then:
r=√2A
Thus, the repulsive force becomes:
FR=k⋅q2(√2A)2=k⋅q22A2
The attractive force FA between the charge Q and the small charge q is also given by Coulomb's law:
FA=k⋅|Q|⋅qA2
Here, A is the distance between Q and q.
For the resultant force on q to be zero, the attractive force FA must equal the repulsive force FR:
FA=FR
Substituting the expressions for FA and FR:
k⋅|Q|⋅qA2=k⋅q22A2
We can cancel k and A2 from both sides (assuming k and A are non-zero):
|Q|⋅q=q22
Dividing both sides by q (assuming q≠0):
|Q|=q2
Since the force between the two small charges q is repulsive, Q must have an opposite sign to q to provide the necessary attractive force. Therefore:
- If q is positive, Q must be negative.
- If q is negative, Q must be positive.
Q = -\frac{q}{2} \quad \text{(if q > 0 )}
or
Q = \frac{|q|}{2} \quad \text{(if q < 0 )}
The value of Q for which the resultant force on q is zero is:
Q = -\frac{q}{2} \quad \text{(if q > 0 )} \quad \text{or} \quad Q = \frac{|q|}{2} \quad \text{(if q < 0 )}
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples
1 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-01
87 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - SUBJECTIVE QUESTION
9 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
Two equal point charges Q=+√2μC are placed at each of the two opposite corners of a square and equal point charges q at each of the other two corners. What must be the value of q so that the resultant force on Q is zero?
View SolutionThree ant P,Q and R are pulling a grain with forces of magnitude 6N,3√3N and 3√2N as shown in the figure. Find the magnitude of resultant force (in N ) acting on the grain .

View Solution
Knowledge Check
A charges Q is placed at each of the two opposite corners of a square. A charge q is placed to each of the other two corners. If the resultant force on each charge q is zero, then
Aq=√2QBq=−√2QCq=2√2QDq=−2√2QThree charges 4q,Q and q are in a straight line in the position of 0.l/2 and l respectively. The resultant force on q will be zero, if Q=
A−qB−2qC−q2D4qTwo particles in air are separated by a certain distance 'R'. Their masses are M1 and M2 and they have equal and similar charges 'Q'. If the resultant force acting among them is zero, then the value of Q is
A√(4πε0GM1M2)B1(4πε0)√(GM1M2)C4πε0GM1M2D1(4πε0)(GM1M2)
Four point charges Q.q Q and q are placed at the corners of a square side 'a' as shown in the figures.

Find the resultant electric force on a charge Q,
View SolutionFour point charges Q, q, Q and q are placed at the corners of a square of side' a' as shown in the figure.
Find the .
(a) resultnat electric force on a charge Q and .
(b) potential energy of this system.
View SolutionTwo forces of magnitudes P and Q are inclined at an angle (θ). The magnitude of their resultant is 3Q. When the inclination is changed to (180∘−θ), the magnitude of the resultant force becomes Q. Find the ratio of the forces.
View SolutionIf resultant of forces acting on a system is zero then
View SolutionCharges Q−q,Q,−q are placed at the corners A,B,C,D of a square respectively. If the resultant force on the charge Q is zero due to other charges, what is the relation between Q and q?
View Solution
