Five point charges, each of value +q are placed on five vertices of a regular hexagon of side Lm. What is the magnitude of the force on a point charge of value -q coulomb placed at the centre of the hexagon?
To find the magnitude of the force on a point charge of value -q placed at the center of a regular hexagon with five point charges of value +q at its vertices, we can follow these steps:
Step 1: Understand the Configuration
We have a regular hexagon with five positive charges (+q) placed at five of its vertices. The sixth vertex is empty. A negative charge (-q) is placed at the center of the hexagon.
Step 2: Calculate the Distance from the Center to the Vertices
The distance from the center of the hexagon to any vertex is equal to the radius of the circumcircle of the hexagon. For a regular hexagon with side length L, this distance (r) can be calculated as:
r=L√3
Step 3: Calculate the Force due to Each Charge
The force exerted on the charge -q at the center by each positive charge +q can be calculated using Coulomb's law:
F=k|q⋅(−q)|r2
Where:
- k is Coulomb's constant,
- r is the distance from the center to a vertex.
Substituting the values:
F=kq2(L√3)2=kq2⋅3L2=3kq2L2
Step 4: Determine the Direction of Each Force
Each positive charge exerts a force directed towards itself on the negative charge. Since the hexagon is symmetrical, we can analyze the forces in pairs:
- The forces from opposite charges will cancel each other out in pairs.
Step 5: Calculate the Net Force
Since there are five charges, we can pair them up. The forces from the two charges that are opposite each other will cancel out. The remaining charge will exert a net force towards the center.
The net force will be the vector sum of the forces from the three remaining charges. The resultant force will be directed towards the vertex of the hexagon that is not occupied by a charge.
Step 6: Final Calculation
The net force on the charge -q is given by the sum of the magnitudes of the forces from the three charges that are not canceled out. The symmetry of the hexagon means that the resultant force will be directed towards the empty vertex.
Thus, the magnitude of the net force Fnet on the charge -q is:
Fnet=3⋅F=3⋅3kq2L2=9kq2L2
Conclusion
The magnitude of the force on the point charge -q placed at the center of the hexagon is:
Fnet=9kq2L2
We have a regular hexagon with five positive charges (+q) placed at five of its vertices. The sixth vertex is empty. A negative charge (-q) is placed at the center of the hexagon.
The distance from the center of the hexagon to any vertex is equal to the radius of the circumcircle of the hexagon. For a regular hexagon with side length L, this distance (r) can be calculated as:
r=L√3
The force exerted on the charge -q at the center by each positive charge +q can be calculated using Coulomb's law:
F=k|q⋅(−q)|r2
Where:
- k is Coulomb's constant,
- r is the distance from the center to a vertex.
F=kq2(L√3)2=kq2⋅3L2=3kq2L2
Each positive charge exerts a force directed towards itself on the negative charge. Since the hexagon is symmetrical, we can analyze the forces in pairs:
- The forces from opposite charges will cancel each other out in pairs.
Since there are five charges, we can pair them up. The forces from the two charges that are opposite each other will cancel out. The remaining charge will exert a net force towards the center.
The net force on the charge -q is given by the sum of the magnitudes of the forces from the three charges that are not canceled out. The symmetry of the hexagon means that the resultant force will be directed towards the empty vertex.
Fnet=3⋅F=3⋅3kq2L2=9kq2L2
The magnitude of the force on the point charge -q placed at the center of the hexagon is:
Fnet=9kq2L2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples1videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-0187videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - SUBJECTIVE QUESTION9videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
Five point charges, each of value +q coul, are placed on five vertices of a regular hexagon of isde L meters. The magnitude of the force on the point charge of value -q coul, placed at the centre of the hexagen is…………….
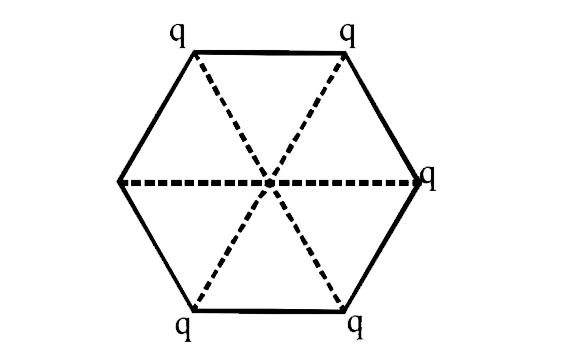 View Solution
View SolutionFive point charges each of charges +q are placed of five vertices of a regular hexagon of side 'l'. Find the magnitude of the resultant force on a charge -q placed at the centre of the hexagon.
(##U_LIK_SP_PHY_XII_C01_E09_018_Q01.png" width="80%">View Solution
Knowledge Check
- Question 1 - Select One
Three point charges each of value +q are placed on three vertices of a square of side a metre. What is the magnitude of the force on a point charge of value −q coulomb placed at the centre of the square?
A(14πε0)(qa)2B(12πε0)(2qa)2C(12πε0)(qa)2D(14πε0)(2qa)2 - Question 2 - Select One or More
Five point charges each of charge + q are placed on five vertices of a regular of side h as shown in the figure. Then
Athe forces on (-q) at O due to charges +q at A and D are balanced.Bthe forces on (-q) due to charges at D and E are balanced.CThe resultant force on −q at O is 14πε0q2h2 along OE.DThe resultant force on - q at O is 14πε0q2h2 along OC. - Question 3 - Select One
Five point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
A14πε0qa2Bq16πε0a2C√2q4πε0a2D5q16πε0a2
Five point charges, each +q are placed on five vertices of a regular hexagon of side' l '. Find the magnitude of the resultant force on a charge –q placed at the centre of the hexagon.
View SolutionFive equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is
 View Solution
View SolutionThe point charges are placed on the vertices of regular hexagon of side L as shown. Find the potential energy of the system of charges.
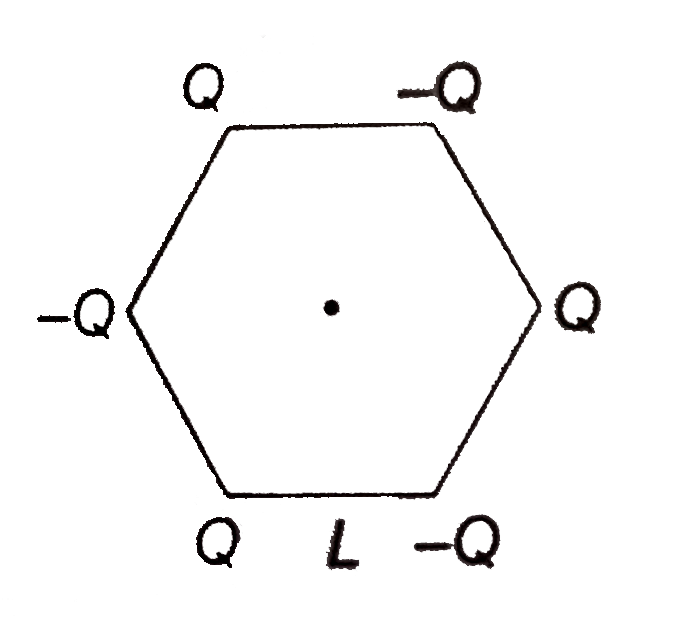 View Solution
View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionFive point charges, +q each are placed at the five vertices of a regular hexagon. The distance of the center of the hexagon from any fo the vertices is a. the electric field at the center of the hexagon is
View Solution

