Column-I show graph of electric potential V versus x and y in a certain region for four situations. Column-II shows the range of angle which the electric field vector makes with positive x-direction

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(A) s, (B) p, (C) r, (D) q

Electric field $\to E = - \frac{\partial V}{\partial x} ˆ i - \frac{\partial V}{\partial y} ˆ j$
For (A): $\to E = - ˆ i + \frac{1}{\sqrt{3}} ˆ j$
For (B): $\to E = + ˆ i$
For (C): $\to E = - ˆ i + \sqrt{3} ˆ j$
For (D): $\to E = + \frac{1}{\sqrt{3}} ˆ i + \sqrt{3} ˆ j$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The figure gives the electric potential $V$ as a function of distance through five regions on x-axis. Which of the following is true for the electric $E$ in these regions ?

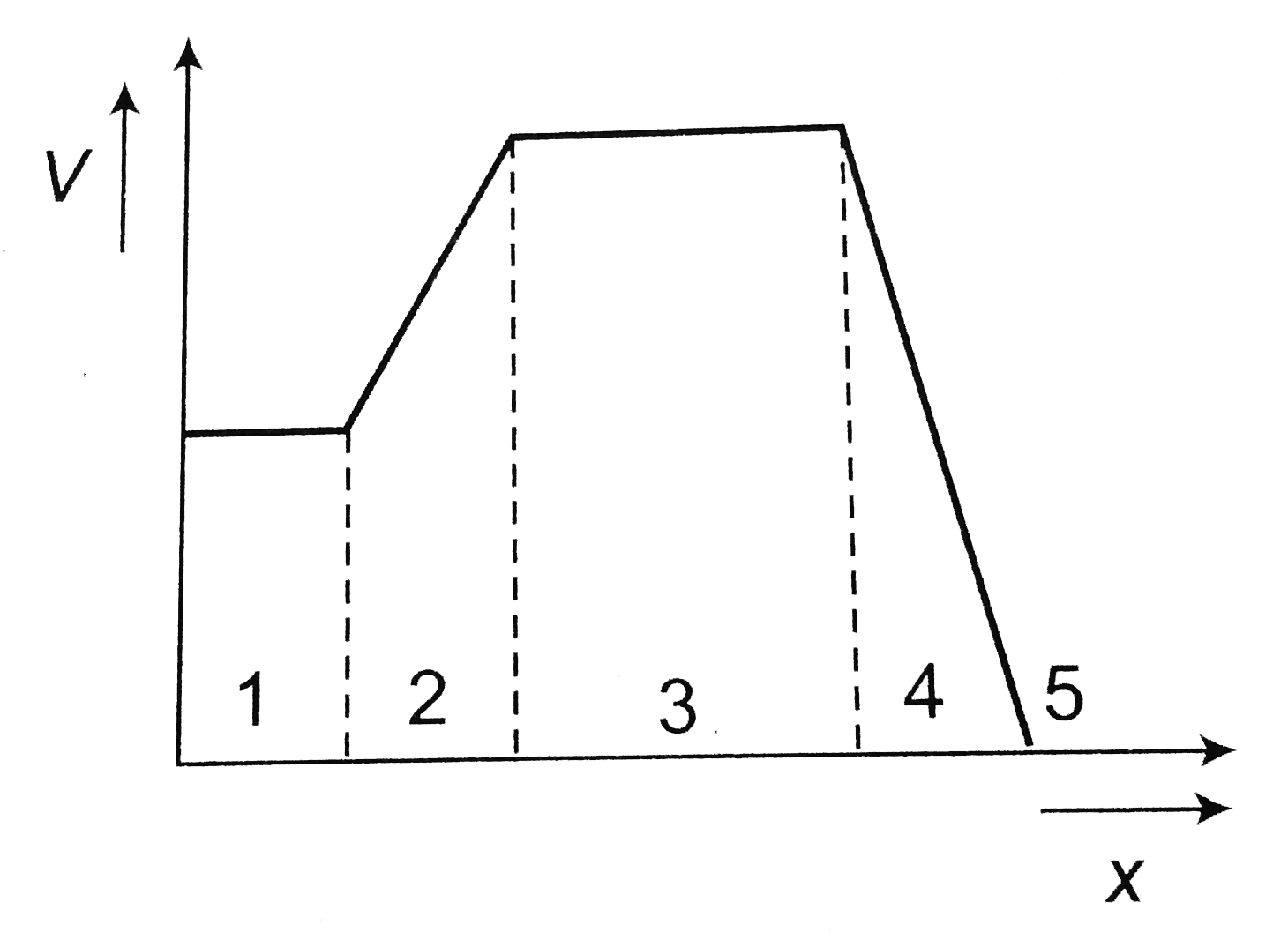A $E_{2} = E_{4}, E_{5} = 0 and E_{3} > E_{1}$
B $E_{1} = E_{3}, E_{5} = 0 and E_{2} < E_{4}$
C $E_{2} = E_{4}, E_{5} = 0 and E_{1} < E_{3}$
D $E_{1} < E_{2} < E_{3} < E_{4} < E_{5}$
Question 2 - Select One
The figure shows the path of a positively charged particle $1$ through a rectangualr region of unifrom electric field as shown in the figure. What is the direction of electric field and the direction of deflection of particles $2, 3$ and $4$ ?
ATop, down, top, down
BTop, down, down, top
CDown, top, top, down
DDiwn, top, down, down

ALLEN-MISCELLANEOUS-Exersice-03

Home
Ask Doubt
Profile