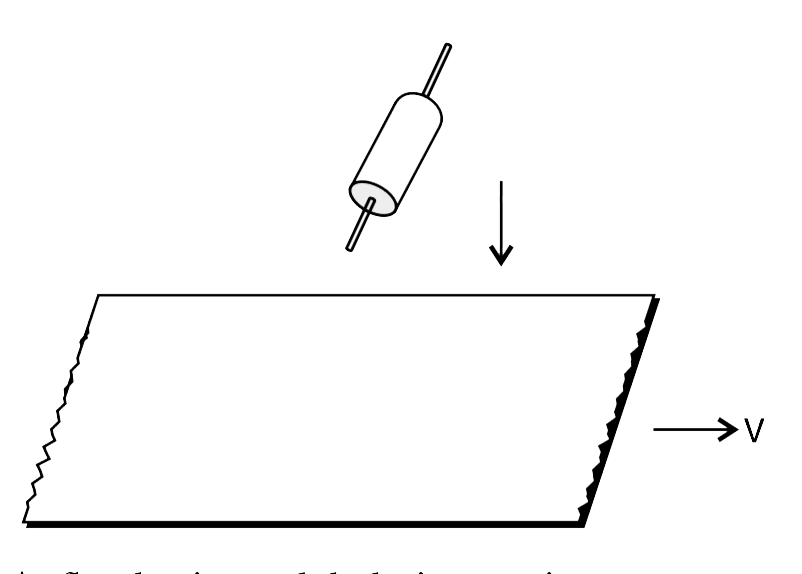
A flat horizontal belt is running at a constant speed V. There is a uniform solid cylinder of mass M which can rotate freely about an axle passing through its centre and parallel to its length. Holding the axle parallel to the width of the belt, the cylinder is lowered on to the belt. The cylinder begins to rotate about its axle and eventually stops slipping. The cylinder is, however, not allowed to move forward by keeping its axle fixed. Assume that the moment of inertia of the cylinder about its axle is $\frac{1}{2} M R^{2}$ where M is its mass and R its radius and also assume that the belt continues to move at constant speed. No vertical force is applied on the axle of the cylinder while holding it.
(a) Calculate the extra power that the motor driving the belt has to spend while the cylinder gains rotational speed. Assume coefficient of friction $= μ$ .
(b) Prove that $50 %$ of the extra work done by the motor after the cylinder is placed over it, is dissipated as heat due to friction between the belt and the cylinder

Text Solution

Verified by Experts

The correct Answer is:(a) $P = μ m g . V$

Updated on:21/07/2023

A cylinder of 500 g and radius 10 cm has moment of inertia about an axis passing through its centre and parallel to its length is
A $2.5 \times 10^{- 3} k g m^{2}$
B $2 \times 10^{- 3} k g m^{2}$
C $5 \times 10^{- 3} k g m^{2}$
D $3.5 \times 10^{- 3} k g m^{2}$
$M . I .$ of a uniform horizontal solid cylinder of mass $M$ about an axis passing through its edge and perpendicular to the axis of cylinder when its length is $6$ times of its radius $R$ is
A $\frac{39}{4} M R^{2}$
B $\frac{39}{2} M R^{2}$
C $\frac{49}{4} M R^{2}$
D $\frac{49}{2} M R^{2}$
The moment f inertia of a solid cylinder about an axis parallel to its length and passing through its centre is equal to its moment of inertia about an axis perpendicular to the length of cylinder and passing through its centre . The ratio of radius of cylinder and its length is
A $1 : \sqrt{2}$
B $1 : 2$
C $1 : \sqrt{3}$
D $1, 3$